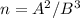За первый час лыжник 10,8 км, за второй 9,5 км и за третий 9,7 км. Сколько километров в среднем проходил - id1779212420230602 от f0xses 02.06.2023 20:21

Question

Математика: За первый час лыжник 10,8 км, за второй 9,5 км и за третий 9,7 км. Сколько километров в среднем проходил лыжник за час?

f0xses · Accepted Answer

Надо доказать, что для любого натурального n можно найти натуральные A и B n = A^2/B^3

, такие что

Заметим, что число n допускает единственное разложение по степеням простых чисел:

$\displaystyle
n = p_1^{m_1}p_2^{m_2}...p_z^{m_z}$

Где p_k

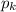- неповторяющиеся простые числа. Построим числа A и B по следующему алгоритму. Примем сначала A=B=1. Для каждого k-го множителя в разложении числа n есть два варианта.

1) если степень m_k

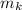четная, домножим число A на 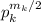$p_k^{m_k/2}$ . Тогда числитель A^2 будет содержать множитель 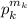$p_k^{m_k}$ , а так как знаменатель B^3 не содержит такого множителя, частное будет тоже содержать множитель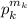 $p_k^{m_k}$

2) если степень m_k

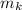нечетная, домножим A на 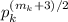$p_k^{(m_k+3)/2}$ , а B домножим на p_k

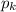. Тогда легко видеть, что отношение A^2 к B^3 будет содержать p_k

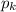в степени

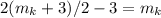, что нам и надо

Действуя таким образом, мы построим нужные нам числа A и B

За первый час лыжник 10,8 км, за второй 9,5 км и за третий 9,7 км. Сколько километров в среднем проходил лыжник за час?

MOGZ ответил