1. Область определения D(f)=(∞;+∞)
2. Область значений Е(f)=(-∞;+∞)
3. Функция ни четная, ни нечетная. т.к. х;-х принадлежат области определения и
f(-x)=-(-x)³-3x+2=x³-3x+2≠-f(x); f(-x)≠f(x), это функция общего вида.
4.у'=(-х³+3х+2)'=-3х²+3=3*(1;-х)(-1+х), исследуя знак производной методом интервалов, ______-1____1_________
- + -
приходим к выводу,что функция убывает на промежутках
(-∞;-1] и [1;+∞) , возрастает на [-1;1].
5.-1 точка минимума,минимум равен 0, х=1- точка максимума, максимум 4.
6. вторая производная у''=-6x=0; x=0 ______0_______
+ -
х=0- точка перегиба, т.к. вторая производная при переходе через нее меняет знак, на промежутке (-∞;0) график выпуклый вниз, на (0;+∞)- вверх.
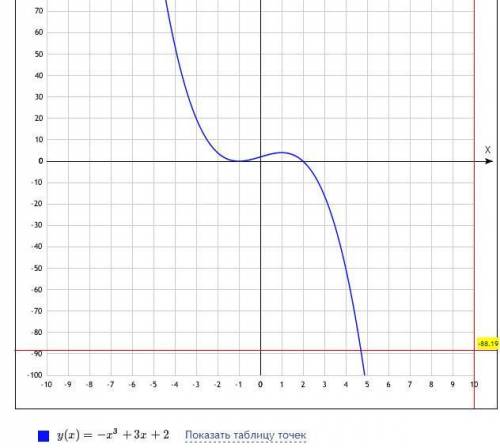
Учитывая полученные результаты, строим график.
4,58-(1,295 +1,936 :3 1/5)×1 16/19+3 5/51:
:(4 5/34-3 19/51)=4,999
1. 1,936 :3 1/5=1,936:3, 2=0,605
(3 1/5=3,2)
2. 1,295 +0,605=1,9
3. 1,9× 1 16/19=1 9/10× 1 16/19=19/10×35/19=
(1,9=1 9/10) =(19×35):(10×19)=7/2 (3,5)
4. 4,58 -3,5= 1,08
5. 4 5/34 - 3 19/51= 1 (7,5/51-19/51)= 1 -11,5/51=
=51/51-11,2/51=39,8 /51=0,78
6. 3 3/51:39,8/51=156/51: 39,8/51=
=(156×51):(51×39,8)=156/39,8=3,919
7. 1,08+3,919 =4,999