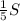 .
.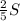 . В эту сумму входит сумма чисел верхнего левого квадрата 2х2, равная 10. Значит, сумма чисел в прямоугольнике высотой 2 и длиной 3 в верхнем правом углу равна
. В эту сумму входит сумма чисел верхнего левого квадрата 2х2, равная 10. Значит, сумма чисел в прямоугольнике высотой 2 и длиной 3 в верхнем правом углу равна 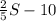 .
.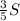 , и в которую входит нижний правый квадрат 3х3 с суммой 15. Уберём из этих нижних трёх строчек квадрат 3х3. Останется прямоугольник высотой 3 и длиной 2, по площади равный верхнему прямоугольнику 2х3, и в которых суммы чисел тоже равны. В нижнем оставшемся прямоугольнике сумма чисел равна
, и в которую входит нижний правый квадрат 3х3 с суммой 15. Уберём из этих нижних трёх строчек квадрат 3х3. Останется прямоугольник высотой 3 и длиной 2, по площади равный верхнему прямоугольнику 2х3, и в которых суммы чисел тоже равны. В нижнем оставшемся прямоугольнике сумма чисел равна 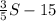 .
.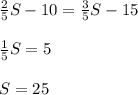
1) 4· 1/3 = 4/3(м³) - накачал 1-й насос
2) 4· 1/5 = 4/5(м³) - накачал 2-й насос
3) 4· 1/7 = 4/7(м³) - накачал 3-й насос
4) 4/3 + 4/5 + 4/7 = 4·(35/105 + 21/105 + 15/105) = 4·71/105 = 284/105 - накачали 3 насоса
5) 4 - 284/105 = 420/105 - 284/105 = 136/105 = 1 31/105 (м³)
или
1) 1/3 + 1/5 + 1/7 = 35/105 + 21/105 + 15/105 = 71/105(часть) накачали 3 насоса вместе
2) 1 - 71/105 = 105/105 - 71/105 = 34/105 (часть) -накачал 4-й насос
3) 4· 34/105 = 136/105 = 1 31/105(м³) - накачал 4-й насос
ответ: 4-й насос накачал 1 31/105 м²