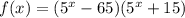
Уравнение касательной имеет вид:
,
где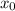 
— абсцисса точки графика функции 
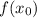, к которому проведена касательная 
.
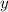Так как график касательной имеет вид график прямой линейной функции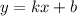 
, а по условию она должна быть горизонтальной, значит, это частый случай линейной функции —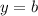 
Таким образом, касательная будет горизонтальной, если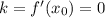 
Найдем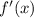 
:
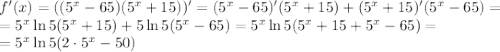
Найдем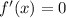 
:
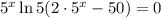
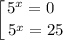
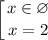
Следовательно,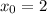 
— абсцисса точки графика функции 
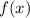, к которому проведена касательная .
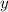Найдем значение :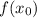
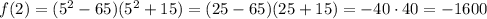
Таким образом,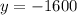 
— уравнение горизонтальной касательной к графику функции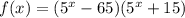
ответ: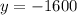
ответ :6823 + 6823 = 13646
Объяснение :Т. к сумма "О" должна давать в сумме двузначное число, "МНОГО" - это пятизначное число. получается что "О" - 5, 6, 7, 8, 9. затем, "О" на конце "МНОГО" и равняется "2хН", значит, "О" - четное число. Для "О" подходит 6 и 8. "М" - это 1.
тогда "Н" равно 2, 3 (если "О"=6) и 6, 7 (для "О"=8).
следует учесть из окончания, что 2х"Н"="О". тогда получается, что "Н"=3, "О"=6. 2х"Д" должно быть двузначным, чтобы "Н"=3.
2х"Д"=6, что допустимо только, если "Д"=3 или 8. 3 уже занято для "Н".