Общая схема исследования и построения графика функции
1. Найти область определения функции и область значений функции, выявить точки разрыва, если они есть.
Область определения функции D(x)( = R.
При определении области значений функции задача сводится к нахождению наибольшего и наименьшего значения функции (это будет в пункте 8).
2. Выяснить, является ли функция четной или нечетной.
Проверим функцию чётна или нечётна с соотношений f = f(-x) и f = -f(-x).
3. Выяснить, является ли функция периодической - нет.
4. Найти точки пересечения графика с осями координат (нули функции).
График функции пересекает ось X при f = 0
значит надо решить уравнение:
5. Найти асимптоты графика - их нет.
6. Вычислить производную функции f'(x) и определить критические точки.
f'(x) = 4х³ - 12х = 4х(х² - 3).
Приравниваем производную нулю: 4х(х² - 3) = 0.
Получаем 3 корня (это критические точки):
х = 0, х = √3 и х = -√3.
7. Найти промежутки монотонности функции.
Исследуем знаки производной:
х = -2 -1.732 -1.5 -0.5 0 0.5 1.5 1.732 28. Определить экстремумы функции f(x).
Где производная меняет знак с - на + там минимум функции, где меняет знак с + на - там максимум.
экстремумы в точках:
(-√ 3, -5) и (√ 3, -5) минимумы.
9. Вычислить вторую производную f''(x).
Приравниваем нулю вторую производную:
f''(x) = 12х²-12 =12(х² - 1) = 0.
Имеем 2 точки перегиба функции: х = 1 и х = -1.
10. Определить направление выпуклости графика и точки перегиба.
Вогнутая на промежутках (-oo, -1] U [1, oo).
Выпуклая на промежутках [-1, 1]
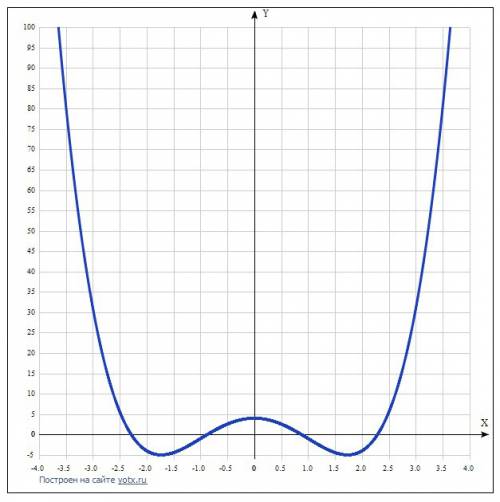
11. Построить график, используя полученные результаты исследования - в приложении.
На заданном интервале графика от -1 до 1 будет только выпуклая его часть.
Пусть ни одно из чисел a и b не делится на 3. Покажем, что если число имеет остаток 1 или 2 при делении на 3, то квадрат этого числа имеет остаток 1 при делении на 3. Действительно, пусть a=3k+1, тогда a²=9k²+6k+1, если a=3k+2, то a²=9k²+18k+4, в обоих случаях остаток равен 1. Но сумма двух чисел с остатком 1 при делении на 3 не может нацело делиться на 3, получили противоречие.
Теперь рассмотрим случай, когда хотя бы одно из чисел a и b делится на 3. Если только одно число делится на 3, то сумма квадратов не будет делиться на 3, то есть, такой вариант невозможен. Остается случай, когда на 3 делятся оба числа. Пусть
Таким образом, уравнение имеет решение лишь при четных n. Следовательно, оно имеет 515 решений, меньших 1031.