7c < 9
c = 0,1
7*0 < 9 0<9
7*1< 9 7 <9
12:d > 3
12:1 >3 12 >3
12:2 > 3 6 > 3
12:3 > 3 4 > 3
d = 1,2,3
Пошаговое объяснение:
6,8x-4=5,7x+6
6,8х - 5,7х= 6 + 4
1,1х= 10
х= 10 : 1,1
х= 10 : 1 1/10
х= 10 : 11/10
х= 10 * 10/11
х= 100/11
х= 9 1/11
равносильное уравнение
2,1х= х+10
2,1х - х= 10
1,1х= 10
х= 10 : 1,1
х= 10 : 1 1/10
х= 10 : 11/10
х= 10 * 10/11
х= 100/11
х= 9 1/11
2)а)
6(3х -4) = 7(2х -3)
18х - 24 =14х - 21
18х - 14х= -21 + 24
4х= 3
х= 3 : 4
х= 0,75
б)
0,6(4х -3) +9,8 = 4(0,6х + 2)
2,4х - 1,8 +9,8 = 2,4х + 8
2,4х - 2,4 х= 8 + 7
0 ≠ 15 не имеет решения
3)|2х−5|= 11
2х -5 = 11 2х- 5= -11
2х= 11 +5 2х = - 11 +5
2х= 16 2х= -6
х1= 8 х2= -3
4)
Пусть в первой коробке - х кг яблок, тогда во второй - 8х кг, когда в первую коробку добавили 9 кг в ней стало х+9 кг, а из второй забрали 26 кг то в ней стало 8х - 26
8х-26= х+9
8х - х= 9 +26
7х= 35
х= 35 : 7
х= 5 кг в первой коробке
14,15 км/час
Пошаговое объяснение:
Пусть скорость катера будет х км/час, тогда его скорость по течению будет (х+3) км/час. Время по течению реки катер затратил 5/ (х+3) час, а по озеру 8/х час. Составим уравнение
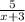 +
+ 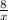 = 1
= 1
5x+8x+24=x(x+3)
12x+24=x²+3x
x²+3x-12x-24=0
x²-9x-24=0
Найдем дискриминант квадратного уравнения:
D = b² - 4ac = (-9)² - 4·1·(-24) = 81 + 96 = 177
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x1 = (9 - √177)/2·1 ≈ -2.1521 не корень
x2 = (9 + √177)/2·1 ≈ 11.152 корень
собственная скорость катера 11,15 км/час
по течению тогда
х+3=11,15+3=14,15 км/час
7*с<9
при c=1 7<9
при c=0 0<9
ответ: 0; 1.
12:d>3
при d=3 12:3>3 4>3
при d=2 12:2>3 6>3
при d=1 12:1>3 12>3
ответ: 1; 2; 3.