4 умножить 3 = 12 киллограм
5 умножить 3 = 15 киллограм
12+15=27 киллограм
ответ: За два дня потратили 27 киллограм краски
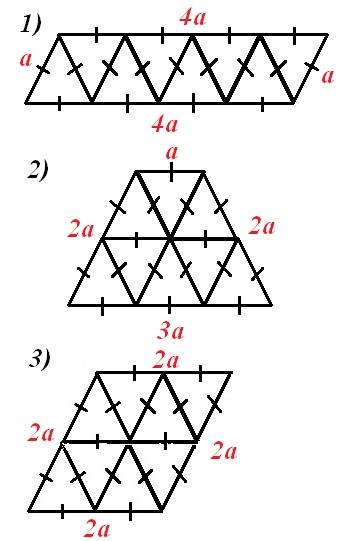
На вскидку сразу смог составить следующие 3 четырехугольника - чертеж во вложении.
Обозначим сторону правильного треугольника через а. В правильном треугольнике все стороны равны и все углы по 60°.
1) Данный четырехугольник - параллелограмм. У него противоположные стороны равны, противолежащие углы равны. Из периметра параллелограмма получим уравнение:
2(а+4а)=16 => a = 1,6 => S параллелограмма = 4a*a*sin60° = (4a²√3)/2 = 2a²√3.
2) Данный четырехугольник - равнобокая трапеция. Из периметра трапеции получим:
а + 2а + 3а + 2а = 16 => a = 2 => S = H(a+3a)/2 = 2aH, где Н - высота трапеции....
Длинц высоты трапеции можно найти как длину высоты равностороннего треугольника со стороной 2а.
По теореме Пифагора: Н² = (2а)² - а² = 3а² => H = a√3
Тогда S трапеции = 2а*a√3 = 2a²√3.
3) Данный четырехугольник - ромб. Его противоположные стороны равны, противоположные углы равны.
4*2а=16 => a = 2 => S ромба = (2а)²sin 60° = 2a²√3.
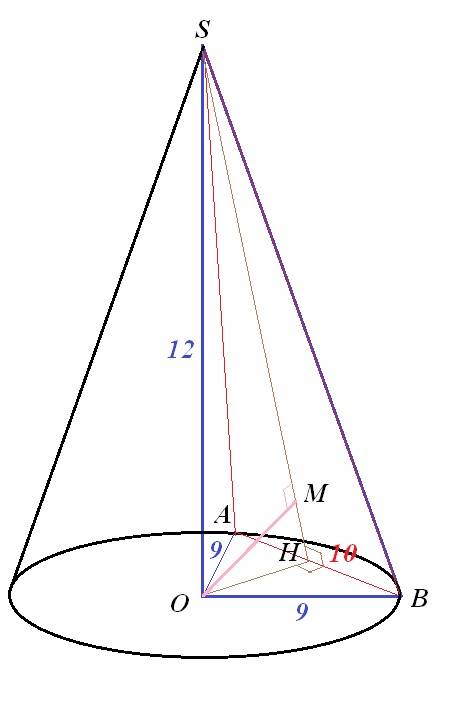
Чертеж к задаче во вложении.
Хорда в основании конуса - отрезок АВ=10.
Плоскость, проходящая через вершину конуса и хорду АВ, это ∆ASB.
Расстояние от О до этого ∆ - это отрезок ОМ. Его и надо найти.
1) ∆АОВ-равнобедренный (ОА=ОВ=9). ОН- мединана, бссектриса, высота ∆АОВ.
АН=ВН=5.
2) По теореме Пифагора в ∆ВОН
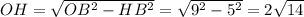
3) По теореме о трех перпендикулярах прямая АВ, проведенная на плоскости через основание Н наклонной SH, перпендикулярна ее проекции ОН, значит АВ перпендикулярна наклонной SH. Тогда в силу того что Н - середина АВ имеем, что SH - и медиана и высота ∆ASB. Т.е. этот треугольник равнобедренный и у него SA=SB.
4) По теореме Пифагора в ∆SОН
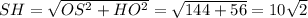
5) Рассмотрим прямоугольный ∆SOH. Пусть НМ = х, тогда SM = 10√2 - х
По теореме Пифагора в ∆МОН
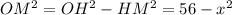
По теореме Пифагора в ∆МОS
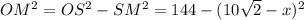
Получаем уравнение:
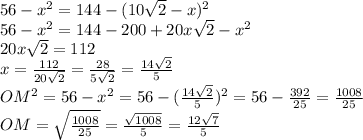
ответ: 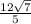
4*3=12кг первый день
5*3=15кг второй
15+12=27кг за два дня банок за два дня
9*3=27кг
или (4+5)*3=27