на 170%
Пошаговое объяснение:
Пусть а и b - стороны треугольника, α - угол между ними. Тогда, площадь треугольника можно вычислить по формуле:
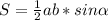
Сторона а, увеличенная на 50% равна а*(100%+50%)/100%=1,5а
Сторона b, увеличенная на 80% равна b*(100%+80%)/100%=1,8b
Площадь полученного треугольника равна
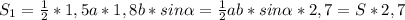
Таким образом, увеличив стороны треугольника на 50% и на 80% соответственно, площадь треугольника увеличилась в 2,7 раза.
2,7*100%=270% - стала равняться площадь треугольника в % по отношению к прежней площади треугольника
270%-100%=170% - на столько % увеличилась площадь треугольника.
Пусть A1 — центр вписанной окружности ∆ SBC, B1 — центр вписанной окружности ∆ SAC, AA1 пересекается с A, A1, B1, B лежат в одной плоскости, значит прямые AB1 и BA1 пересекаются на ребре SC. Пусть точка пересечения этих прямых — p. Так как Ap и Bp — биссектрисы углов A и B, то . Но тогда AC • BS = BC • AS, отсюда , следовательно биссектрисы углов S в ∆ ASB и C в ∆ ACB пересекаются на ребре AB, т.е. точки S, C и центры вписанных окружностей ∆ ASB и ∆ ACB лежат в одной плоскости. Отсюда следует, что отрезки, соединяющие вершины S и C с центрами вписанных окружностей противолежащих граней, пересекаются.
Пошаговое объяснение:
Пошаговое объяснение:
2x+ x + x+ 4 = 300
4x=296
x=74 это второй мальчик
первый 74*2=148
третий 74+4= 78