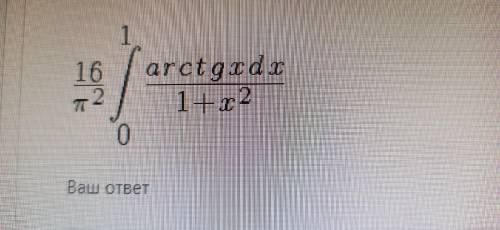
1) По графику определите, у которого из автомобилей в начальный момент времени скорость больше?
Решение. По графику видно, что в начальный момент времени 0 (выделен красным) скорости автомобилей равны, соответственно, υ₁ = 90 км/ч и υ₂ = 60 км/ч. Тогда
υ₁ = 90 км/ч > υ₂ = 60 км/ч.
ответ: В начальный момент времени у первого из автомобилей скорость больше.
2) По графику определите, у которого из автомобилей в момент времени 6 (ч) скорость больше?
Решение. По графику видно, что в начальный момент времени 6 (ч) (выделен синим) скорости автомобилей равны, соответственно, υ₁ ≈ 110 км/ч и υ₂ = 150 км/ч. Тогда
υ₁ ≈ 110 км/ч < υ₂ = 150 км/ч.
ответ: В момент времени 6 (ч) у второго из автомобилей скорость больше.
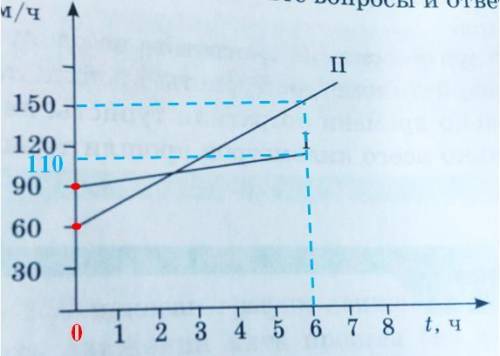
Пошаговое объяснение:
а) разделил на 2 интеграла по разности, под первым e^(pi) - константа, поэтому получится e^(pi) * x = pi* e^(pi) - 0 ( при подстановке)
второй - табличный = sinx + C = 0 в подстановке.
ответ: pi* e^(pi)
б) занесу cosx под дифференциал
cosxdx = d ( sinx + 1)
дальше простой степенной интеграл = 1/3*(1+sinx)^3 + C = 1/3 * (1)^3 - 1/3 * (1)^3 = 0
в) опять под дифференциал
d(4-t^2) = -2*t dt => tdt = -1/2 * d(4-t^2)
дальше простой степенной интеграл = -1/2*2*(4-t)^(1/2) + C = -3^(1/2) + 4^(1/2) = 2 - 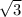
г) под дифференциал:
d(1 + 4x^3) = 12x^2 dx => 6x^2dx = 1/2 d(1+4x^3)
дальше табличный интеграл = 1/2 * ln(1+4x^3) + C = 1/2*ln5 - 1/2*ln1 = 1/2*ln5
Пошаговое объяснение: