Деревянная балка имеет форму прямой призмы. Еe основание равносторонний треугольник, длина стороны которого равна 15 см. Степан эту балку разрезал на 6 одинаковых кусков. Затем их сложил так, как показано на рисунке справа, и скрепил их металлической лентой в две полосы. Полученное тело имеет форму призмы, у которой все боковые грани-квадраты.
1) Найдите длину балки.
2) Найдите сумму длин всех боковых ребер призмы. 3) Сколько сантиметров металлической ленты израсходовал Степан, если при соединении ленты он концы накладывал один на другой, а длина двойной части равна 3 см?

👇

Открыть все ответы

Ответ:

arehovaa1

25.11.2021

Растительность африканских пустынь чрезвычайно скудна и состоит в основном из скопления трав и точечных произрастаний кустарников и деревьев в оазисах, вдоль воды и в высотных районах. В оазисах Сахары растет уникальная Финиковая пальма Эрг-Шебби. Во впадинах встречаются необычные растения галофиты, устойчивые к соли. Растительность пустынных областей давно при к нерегулярности осадков и засухам. Это заметно по разнообразию их физиологических адаптаций, предпочтению мест обитания, созданию сообществ и стратегий размножения.
В горных районах Сахары можно встретить реликтовую неогеновую флору и множество эндемичных видов. Так здесь встречаются реликтовые древесные растения: олива, кипарис, мастиковое дерево. Помимо этого в горах Сахары произрастают акации, тамариски, полынь, эфедра, дум-пальма, олеандр, тимьян и финик пальчатый. В оазисах люди научились возделывать инжир, оливы, фруктовые деревья, цитрусовые и всевозможные овощи. Травянистые растения, расположившиеся во всех частях пустыни – это триостница, просо и полевичка. Прибрежница и другие устойчивые к солям травы растут на берегу Атлантического океана. Сообщества эфемеров формируют сезонные пастбища - ашебы. В водоёмах можно увидеть водоросли.
Необычное растение пустыни Намиб - Вельвичия (Тумбоа) , всю свою жизнь, а это более 1000 лет, отращивающее два гигантских листа, которые впоследствии превышают 3 м в длину. Листья его крепятся к стеблю, напоминающему гигантскую редиску диаметром 60-120 см, торчащему из земли на 30 см. Корни Вельвичии длинной до 3 м. Вельвичия растет, используя росу и туман как единственные источники влаги в пустыне.
Еще одно известное растение Намиба — нара растёт в чуть более влажных песчаных дюнах. Её плоды являются источником влаги и пищи для многих животных, антилоп, дикобразов, слонов и пр.

4,6(77 оценок)

Ответ:

Adamant0813

25.11.2021

Задание № 1:

На сколько нулей оканчивается значение произведения 20^50*50^20?

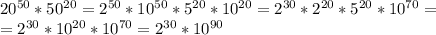
$20^{50}*50^{20}=2^{50}*10^{50}*5^{20}*10^{20}=
2^{30}*2^{20}*5^{20}*10^{70}= \\ =2^{30}*10^{20}*10^{70}=2^{30}*10^{90}$

2 в некой степени, очевидно, не заканчивается на 0. Значит, число нулей - 90.

ОТВЕТ: 90

Задание № 2:

Сколько существует двузначных чисел, которые после перестановки цифр увеличиваются на 75%?

РЕШЕНИЕ: Пусть было число АВ=10а+b. После перестановки получили число BA=10b+a. По условию:

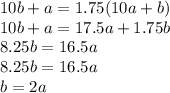
$10b+a=1.75(10a+b) \\ 10b+a=17.5a+1.75b \\ 8.25b=16.5a
\\ 8.25b=16.5a \\ b=2a$

Значит, если в числе цифра десятков в 2 раза больше цифры единиц, то оно попадает под наше условие.

Это числа: 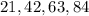21, 42, 63, 84

ОТВЕТ: 4 числа

Задание № 3:

Решите уравнение: |||x|−5|−5|=5. Назовите наибольший корень уравнения.

$|||x|-5|-5|=5 \\ \left[\begin{array}{l} ||x|-5|-5=5 \\
||x|-5|-5=-5\end{array} \\ \left[\begin{array}{l} ||x|-5|=10 \\
||x|-5|=0\end{array} \\ \left[\begin{array}{l} |x|-5=10 \\ |x|-5=-10 \\
|x|-5=0\end{array}$

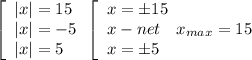
$\left[\begin{array}{l} |x|=15 \\ |x|=-5 \\
|x|=5\end{array} \left[\begin{array}{l} x=\pm15 \\ x - net \\ x=\pm5\end{array}
x_{max}=15$

ОТВЕТ: 15

Задание № 4:

В коробке лежат чёрные, белые и красные шарики. Чёрных больше, чем 7, а белых меньше, чем 7. Вместе чёрных и красных в 2 раза больше, чем белых, а белых и красных ровно столько, сколько чёрных. Сколько всего шариков?

РЕШЕНИЕ: Пусть черных с, белых b, красных k.

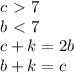
$c\ \textgreater \ 7 \\ b\ \textless \ 7 \\ c+k=2b \\
b+k=c$

Складываем уравнения:

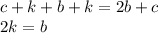
$c+k+b+k=2b+c \\ 2k=b$

Подставляем во второе:

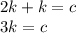
$2k+k=c \\ 3k=c$

$\left \{ {{3k\
\textgreater \ 7 } \atop {2k\ \textless \ 7}} \right. \\ \left \{ {{k\
\textgreater \ 7/3 } \atop {k\ \textless \ 7/2}} \right.$

Единственное возможное целое k - число 3.

Тогда k+c+b=k+3k+2k=6k=6*3=18 шариков

ОТВЕТ: 18 шариков

Задание № 5:

Стоя неподвижно на ступени эскалатора в метро Ваня поднимается наверх за одну минуту. Взбегая по ступеням неподвижного эскалатора, он добирается до верха за 40 секунд. За какое время Ваня поднимается наверх, если начинает взбегать по ступеням эскалатора, движущегося вверх? Дайте ответ в секундах.

РЕШЕНИЕ: Пусть длина расстояния L.

Если Ваня стоит неподвижно на ступени эскалатора, то скорость движения равна L/60. (Считаем в секундах, в минуте 60 секунд).

Если Ваня взбегает по ступеням неподвижного эскалатора, то скорость движения равна L/40.

Когда Ваня бежит по ступеням движущегося эскалатора, то скорости Вани и эскалатора суммируются: L/60+L/40. Тогда время определяется отношением длины к скорости:

$\frac{L}{ \frac{L}{60} + \frac{L}{40} } = \frac{1}{
\frac{1}{60} + \frac{1}{40} } = \frac{1}{ \frac{2}{120} + \frac{3}{120} }
=\frac{1}{ \frac{5}{120} } =\frac{120}{5}=24$

ОТВЕТ: 24 секунды

Задание № 6:

Встретились три охотника и сварили кашу. Первый дал две кружки крупы, второй — три кружки крупы, а у третьего крупы не было. Но зато он дал охотникам 30 рублей в качестве платы за кашу. Все кашу ели поровну. Сколько рублей достанется второму охотнику, если их разделить по справедливости?

РЕШЕНИЕ: Так как 3 порции каши готовились из 5 кружек крупы, то одна порция составляет (5/3) кружки.

Первый дал две кружки крупы, значит, он имел право получить две кружки каши. Однако он взял только (5/3) кружки. 2-5/3=1/3 кружки – первый передал третьему

Второй дал три кружки крупы, значит, он имел право получить три кружки каши. Однако он взял только (5/3) кружки. 3-5/3=4/3 кружки – второй передал третьему

Видно, что второй передал третьему в 4 раза больше каши, чем первый. Значит и денег он получит в 4 раза больше. Деньги делим в отношении 1:4, то есть всего 5 частей. 30/5*4=24 рубля

ОТВЕТ: 24 рубля

Задание № 7:

Отрезок 50 см разделён на четыре неравных отрезка. Расстояние между серединами средних отрезков равно 10 см. Найдите расстояние между серединами крайних отрезков. Дайте ответ в сантиметрах.

РЕШЕНИЕ: Расстояние между серединами крайних отрезков представляет собой полусумму длин крайних отрезков и сумму длин средних отрезков.

Так как расстояние между серединами средних отрезков равно 10 см, то сумма их длин равна 2*10=20 см.

Оставшаяся длина – это сумма длин крайних отрезков: 50-20=30 см. Их полусумма тогда равна 30/2=15 см

20+15=35 см

ОТВЕТ: 35 см

4,8(61 оценок)

Это интересно:

17.04.2022

Как избежать наказания в школе: 10 простых советов...

Праздники-и-традиции

24.12.2020

Как правильно чистить искуственную елку...