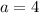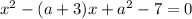
Воспользуемся теоремой Виета:
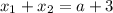
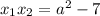
Произведение корней 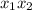 на 2 больше суммы
на 2 больше суммы 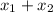 этих корней, следовательно:
этих корней, следовательно:
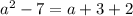
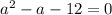
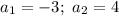
Определим, при каких значениях параметра  данное уравнение существует.
данное уравнение существует.
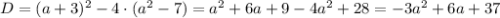
Следовательно, 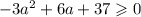 — условие существования корней данного квадратного уравнения.
— условие существования корней данного квадратного уравнения.
Проверим, удовлетворяют ли полученные значения параметров для решения исходного уравнения.
Если 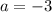 , то получаем неправильное неравенство
, то получаем неправильное неравенство 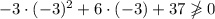
Если 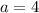 , то получаем верное неравенство
, то получаем верное неравенство 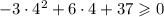
Таким образом, только 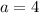 обратит данное уравнение в таковое, что произведение корней на 2 будет больше суммы этих корней.
обратит данное уравнение в таковое, что произведение корней на 2 будет больше суммы этих корней.
ответ: 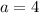
Воспользуемся теоремой Виета:
Произведение корней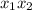 на 2 больше суммы
на 2 больше суммы 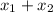 этих корней, следовательно:
этих корней, следовательно:
Определим, при каких значениях параметра данное уравнение существует.
данное уравнение существует.
Следовательно,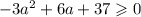 — условие существования корней данного квадратного уравнения.
— условие существования корней данного квадратного уравнения.
Проверим, удовлетворяют ли полученные значения параметров для решения исходного уравнения.
Если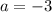 , то получаем неправильное неравенство
, то получаем неправильное неравенство 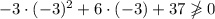
Если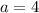 , то получаем верное неравенство
, то получаем верное неравенство 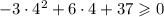
Таким образом, только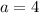 обратит данное уравнение в таковое, что произведение корней на 2 будет больше суммы этих корней.
обратит данное уравнение в таковое, что произведение корней на 2 будет больше суммы этих корней.
ответ: