пусть скорости ИМ - 1/х, ДН - 1/у, АП - 1/z
тогда по условию:
1/x + 1/y = 1/20
1/y + 1/z = 1/24
1/x + 1/z = 1/30
сложим все уравнения:
2(1/x + 1/y + 1/z) = 1/20 + 1/24 + 1/30 = 1/8
1/x + 1/y + 1/z = 1/16 => за 16 часов они втроем разгромят войско
ответ: за 16 часов
2. переведем в минуты:
9 ч 36 мин = 576 мин
1 ч 12 мин = 72 мин
6 ч = 360 мин
1) 2400 : 576 * 72 = 300 (л) - наполнил первый
2) 2400 - 300 = 2100 (л) - осталось наполнить второму
3) 360 : 2400 = 0,15 (мин) - за столько второй наполняет 1 л
4) 0,15 * 2100 = 315 (мин) - столько должен работать второй насос
315 мин = 5 часов 15 минут
ответ: 5 часов 15 минут = 5,25 часов
Пусть сделано 2k-1 ходов. Тогда последним сделал ход первый. Пусть они оба начинали с числа n. Тогда на 2k-1 ходу получилось число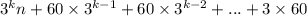
; Упростим это выражение с формулы суммы геометрической прогрессии со знаменателем 3, имеем: 
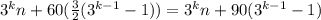; Пусть это число оказалось равным A; То есть 
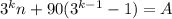;Общее решение этого уравнения:
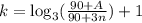; При этом будем стараться искать наименьшее значение n; Заметим, что знаменатель дроби в логарифме больше 90. Если результат k≥4, то числитель дроби в логарифме слишком большой. Больше 1000, а значит мы пропустили чей-то выигрыш. Тогда k=3; Результат 90+A должен быть таким, что ход второго (а это прибавление 60) выходил за интервал. То есть 90+A>1000-60+90=1030; Поскольку k=2, то 90+A=9(90+3n); Решим неравенство: 9(90+3n)>1030, откуда x>220/27, значит x≥9. Наименьшее значение n равно 9. В этом несложно убедиться. ответ: 9