Поскольку n ≥ 1 (как натуральное число), n + 2 > 0, n + 1 > 0. Тогда — каждый следующий член строго больше предыдущего, значит, последовательность строго возрастает.
3) Поскольку последовательность строго возрастает, она ограничена снизу первым членом. Проверим ограниченность сверху:
Последовательность ограничена сверху. Поскольку она ограничена и сверху, и снизу, то она ограниченная.
1. Что называется объемом понятия? Приведите пример трех объектов, принадлежащих объему понятия "треугольник" и трех объектов, не принадлежащих объему данного понятия. 2. Назовите понятие, которое является родовым по отношению к данным: подосиновики, опята, сыроежки. 3. Что называется определением понятия? 4. Какие виды определений понятий чаще всего применяются при формировании у дошкольников начальных математических представлений? Приведите пример. 5. Проведите логический анализ определения понятия: "Значение переменной, при котором уравнение превращается в верное равенство, называется корнем уравнения". 6. А - множество букв в слове "грамматика"; В - множество букв в слове "математика". Найти: АВ, АВ, А\В, АхВ. 7. Правильна ли классификация: Множество многоугольников разбивается на подмножества правильных четырехугольников, шестиугольников и квадратов. 8. Придумайте задание для дошкольников на разбиение множества на классы. 9. Даны множества: А= {2, 4, 6, 8, 10} и В= {1, 3, 5, 7}, элементы которых находятся в соответствии R: «число а меньше числа в», причем аА, вВ. Постройте граф соответствия R, перечислите все пары чисел, находящиеся в соответствии R. 10. Приведите пример задания для дошкольников, выполняя которое они устанавливают соответствие между двумя множествами. 11. На множестве Х={1, 2, 3, 4, 5, 6, 7, 8, 9} задано отношение R: «быть больше на 2». Постройте граф отношения R. Является ли данное отношение отношением порядка? ответ обосновать. 12. Придумайте задание для дошкольников на упорядочение множеств
1) x₁ = 1,5; x₄ = 2,4; x₉ = 2,7; x₉₉ = 2,97; x₉₉₉ = 2,997;
2) строго возрастает;
3) ограничена.
Пошаговое объяснение:
1)
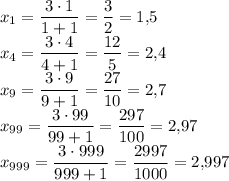
2) Оценим разность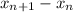
:
Поскольку n ≥ 1 (как натуральное число), n + 2 > 0, n + 1 > 0. Тогда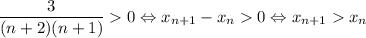
— каждый следующий член строго больше предыдущего, значит, последовательность строго возрастает.
3) Поскольку последовательность строго возрастает, она ограничена снизу первым членом. Проверим ограниченность сверху:
Последовательность ограничена сверху. Поскольку она ограничена и сверху, и снизу, то она ограниченная.