Выбираем систему координат так, чтобы её начало совпадало с положением автомобиля, находящегося в точке А. Уравнение его движения х 1 = v1t. Тогда уравнение движения второго автомобиля х 2 =x0 +v2t. В некоторый момент времени координаты движущихся автомобилей будут одинаковы х1 = х2. Тогда v1t. = x0 +v2t. ю Отсюда t = x0/(v1 - v2). Вычислим: t = 150/(70 - 40) = 5 (часов) . Подставим. Второй автомобиль двигался из точки В со скоростью 40 км/ч. За 5 ч от путь S = 40*5 = 200 (км) . Можно решить задачу и арифметически: 1). С какой скоростью первый автомобиль догоняет второго? 70 - 40 = 30 (км/ч). 2). За сколько времени он его догонит? 150: 30 = 5 (часов) . 3). На какое расстояние он удалится? 40*5 = 200 (км) . ответ: 200 км. через 5 часов.
Правильная четырехугольная пирамида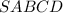 .
.
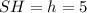 (см).
(см).
Найти: - сторону основания.
- сторону основания.
Решение:Площадь боковой поверхности правильной четырехугольной пирамиды можно вычислить по следующей формуле:
Попробуем выразить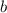 через
через  (сторону основания) и
(сторону основания) и 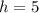 (см) (высоту пирамиды).
(см) (высоту пирамиды).
Рассмотрим прямоугольный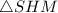 (где
(где 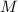 - середина
- середина 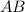 ). В нем
). В нем 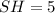 (см), а
(см), а 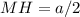 (см) (как половина стороны квадрата, равной
(см) (как половина стороны квадрата, равной  см).
см).
По теореме Пифагора:
Все это подставляем в уравнение площади боковой поверхности (при возведении в квадрат держим в голове, что - неотрицательное):
- неотрицательное):
Пусть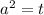 :
:
Второй корень нам не подходит по причине отрицательности. Значит:
Задача решена!
ответ: