Всего 6 рисунков
Пошаговое объяснение:
Число различных рисунков есть то же самое, что и количество различных сочетаний (перестановок) групп по три из трех.
Всего таковых насчитывается 3! (читается как три факториал, а считается как произведение всех натуральных чисел от одного до в данном случае трех)
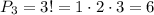
Кратко докажем что это так:
Будем закрашивать в конкретном порядке:
(голова(Г) -> крылья(К) -> хвост(Х))
Г - закрашиваем любыми цветами - их 3
К - закрашиваем любым из оставшихся - их 2
Х - закрашиваем единственным оставшимся - он 1
Отсюда и число сочетаний
Для каждого из 3 разных варианта Г есть по 2 варианта К (мы ведь уже использовали одну краску, т.е. две осталось); итого 3*2=6 вариантов.
И для каждого из 6 вариантов существует по единственному варианту Х (две краски из трех ведь мы использовали)
Итого и получаем 3*2*1 = 1*2*3 = 3! = 6 вариантов рисунков всего
Всего 6 рисунков
Пошаговое объяснение:
Число различных рисунков есть то же самое, что и количество различных сочетаний (перестановок) групп по три из трех.
Всего таковых насчитывается 3! (читается как три факториал, а считается как произведение всех натуральных чисел от одного до в данном случае трех)
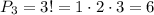
Кратко докажем что это так:
Будем закрашивать в конкретном порядке:
(голова(Г) -> крылья(К) -> хвост(Х))
Г - закрашиваем любыми цветами - их 3
К - закрашиваем любым из оставшихся - их 2
Х - закрашиваем единственным оставшимся - он 1
Отсюда и число сочетаний
Для каждого из 3 разных варианта Г есть по 2 варианта К (мы ведь уже использовали одну краску, т.е. две осталось); итого 3*2=6 вариантов.
И для каждого из 6 вариантов существует по единственному варианту Х (две краски из трех ведь мы использовали)
Итого и получаем 3*2*1 = 1*2*3 = 3! = 6 вариантов рисунков всего
Запись, состоящая из чисел и малых букв латинского алфавита, связанных между собой знаками арифметических действий называется буквенным выражением. В этой записи могут присутствовать скобки. Например, запись a + b – 3 ∙ c является буквенным выражением. Вместо букв в буквенное выражение можно подставлять различные числа. При этом значение букв может изменяться, поэтому буквы в буквенном выражении называют еще переменными.
Подставив в буквенное выражение числа вместо букв и вычислив значение получившегося числового выражения, находят значение буквенного выражения при данных значениях букв (при данных значениях переменных). В таблице 2 приведены примеры буквенных выражений.
Буквенное выражение может не иметь значения, если при подстановке значений букв получается числовое выражение, значение которого для натуральных чисел не может быть найдено. Такое числовое выражение называется некорректным для натуральных чисел. Говорят также, что значение такого выражения «не определено» для натуральных чисел, а само выражение «не имеет смысла». Например, буквенное выражение a – b не имеет значения при a = 10 и b = 17. Действительно, для натуральных чисел, уменьшаемое не может быть меньше вычитаемого. Например, имея всего 10 яблок (a = 10), нельзя отдать из них 17 (b = 17)!
В таблице 2 (колонка 2) приведён пример буквенного