Задание № 1:
Сколько существует различных шестизначных чисел, у которых третья цифра 3, пятая цифра 5, а остальные цифры чётные? Цифры в записи числа не должны повторяться.
на первом месте любая четная цифра кроме нуля (2468) - 4 варианта
на втором месте любая четная цифра (02468), кроме одной использованной раньше - 4 варианта
на четвертом месте любая четная цифра (02468), кроме двух использованных раньше - 3 варианта
на шестом месте любая четная цифра (02468), кроме трех использованных раньше - 2 варианта
4*4*3*2=96
ответ: 96
Задание № 2:
Пишутся одно за другим подряд числа натурального ряда 12345678910111213... Какая цифра будет записана на 333 месте?
для однозначных нужно 1*9=9 цифр
для двузначных нужно 2*90=180 цифр
итого для одно- и двузначных 9+180=189
осталось для трехзначных 333-189=144
в каждом числе по три цифры - 144/3=48 числа запишется
эти числа 100, 101, ..., 147 - последняя цифра 7
ответ: 7
Задание № 3:
Какое число надо прибавить к числителю дроби 23/55 и вычесть из её знаменателя, чтобы получилась дробь 9/17?
это число х
(23+х)/(55-х)=9/17
17(23+х)=9(55-х)
391+17х=495-9х
26х=104
х=4
ответ: 4
Задание № 4:
В коробке 5 красных, 6 зелёных, 7 синих и 8 жёлтых карандашей. В темноте из коробки берут карандаши. Какое наименьшее число карандашей надо взять, чтобы среди них обязательно было 3 карандаша одного цвета?
в худшем случае достанем по 2 карандаша каждого цвета, цветов четыре, то есть карандашей 2*4=8
девятый для какого-то цвета будет третьим
ответ: 9
Задание № 5:
Турист, проплывая против течения под мостом, потерял кепку. Через 20 минут он заметил пропажу, развернулся и поймал кепку в 4 км от моста. Какова скорость течения реки? Дайте ответ в километрах в час.
так как и кепка и турист плывут по одному течению, то туристу для возвращения к кепке понадобится столько же времени, то есть 20 минут
итого турист добрался до кепки через 20+20=40 минут после потери
кепка проплыла 4 км
4км/40мин=4км/(2/3)ч=6км/ч
ответ: 6
Задание № 6:
В трёх корзинах лежат яблоки. В первой на 10 яблок меньше, чем в двух других вместе, а во второй на 16 яблок меньше, чем в первом и третьем. Сколько яблок в третьей корзине?
в первом х, во втором у, в третьем z
x=y+z-10
y=x+z-16
подставим первое во второе
y=y+z-10+z-16
0=z-10+z-16
2z=26
z=13
ответ: 13
Задание № 7:
Расшифруйте запись: 7ABCDE:5=ABCDE7. Одинаковые буквы - это одинаковые цифры, разные буквы - разные цифры. Найдите значение суммы: A+B+C+D+E
перепишем пример через умножение
ABCDE7*5=7ABCDE
E=5
ABCD57*5=7ABCD5
D=8
ABC857*5=7ABC85
C=2
AB2857*5=7AB285
B=4
A42857*5=7A4285
A=1
1+4+2+8+5=20
ответ: 20
ДАНО
Y = (x² + 9)/x
ИССЛЕДОВАНИЕ
1. Область определения. Деление на ноль в знаменателе.
Х≠ 1.
Х∈(-∞;0)∪(0;+∞)
2. Вертикальная асимптота: Х= 1.
3. Пересечение с осью Х. Y(x) = 0 - нет.
4. Пересечение с осью У - нет
5. Наклонная асимптота
k = lim(+∞)Y(x)/x = 4*x/x = 4. Уравнение асимптоты: Y = 4*x.
6. Проверка на чётность.
Y(-x) ≠ Y(x). Y(-x) ≠ - Y(x)
Функция ни четная ни нечетная.
7. Поведение в точке разрыва.
lim(->0-) Y(x) = -∞.
lim(->0+) Y(x) = +∞
8, Первая производная.
6. Локальные экстремумы.
Y'(x) = 0, x1 = - 3/2, x2 = 3/2
Максимум Y(-3/2)= .-12.
Минимум Y(3/2) = 12.
7. Участки монотонности функции.
Возрастает - Х∈(-∞;-3/2]∪[3/2;+∞).
Убывает - Х∈[-3/2;0)∪(0;3/2]
8. Вторая производная.
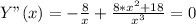
Корней нет. Точек перегиба (на графике) - нет.
9. Выпуклая - "горка" - Х∈(-∞;0). Вогнутая - "ложка" - Х∈(0;+∞)
10. График в приложении

(564+128)-245=447
(645-218)+(241+92)=760
1000-(625-128)=503
(168+120)+240=528