Нам надо изучать разложение на простые множители самих чисел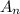 
Отметим, что в пределах до 1000 никакое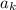 
не может быть больше 9.
Случай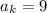 
достигается для числа n=512. Но даже 2 в 10-й степени уже больше 1000. Все меньшие 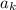также достигаются по крайней мере для соответствующих степеней двойки.
Значит какой бы ни был этот НОК, он представим в виде
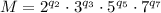
Где соответствующие q - максимальные среди степеней соответствующих простых множителей (2, 3, 5, 7) в разложении чисел .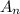
Очевидно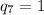 
, потому что даже 2^7 * 3^7 > 1000. Аналогично 
.
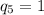Кубов в разложении n не больше двух, поскольку даже
2^3 * 3^3 * 5^3>1000,
но 2^3 * 3^3<1000. Мы бы могли попробовать увеличить количество троек, не добавляя новых простых чисел вроде 5 и более, а комбинируя кубы и девятые степени маленьких, но знаем, что соответствующие n точно будут больше 1000. Шестые и девятые степени комбинировать еще бессмыссленне. Значит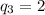 
Точно также, квадратов в разложении n не больше трех, ибо 2^2*3^2*5^2=900<1000, но 2^2*3^2*5^2*7^2>1000. Заменить какой-либо квадрат даже на четвертую степень мы уже не можем. Попытка отбросить 5^2 и сделать обе степени четвертыми (min 1296), или одну восьмой а вторую квадратом (min 2304) тоже выводят за 1000. Значит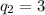 
Окончательно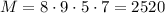 
6 гяпик
Пошаговое объяснение:
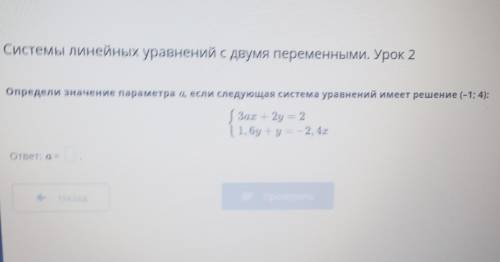
пусть 1 тетрадь=х, а 1 линейка=у. Тогда резинка= 1/2х и 1/4у Так как за всё было оплачено 51 гяпик, составим систему уравнений:
1/2х+2х+3у=51 |×2
1/4у+3у+2х=51 |×4
х+4х+6у=102
у+12у+8х=204
5х=102–6у
13у+8х=204
х=(102–6у)÷5
13у+8х=204
х=20,4–1,2у
13у+8х=204
теперь подставим значение х во второе уравнение:
13у+8х=204
13у+8(20,4–1,2у)=204
13у+163,20–9,6у=204
3,4у=204–163,20
3,4у=40,80
у=40,80÷3,4=12
Итак: линейка стоит 12 (гяп)
Теперь подставим значение у в первое уравнение:
х=20,4–1,2у=20,4–1,2×12=20,4–14,4=6(гяп)
Тетрадь стоит 6(гяп)
тогда резинка стоит: 1/2х=½×6=3(гяп)