Запишите все двухзначные числа,в запись которых входят лишь цифры 2 и 3.найдите сумму этих чисел!

👇

Увидеть ответ

Ответ:

bhgd

03.08.2020

23,32(если можно повторять цифры то 22,33)

23+32=55(если с повтором то 23+32+22+33=110)

4,7(33 оценок)

Ответ:

гриша882

03.08.2020

12,13,22,21,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,42,43,52,53,62,63,72,73,82,83,92,93

сумма равна 1425

4,8(89 оценок)

Открыть все ответы

Ответ:

Zaher11

03.08.2020

Пошаговое объяснение:Определите верно ли данное высказывание

Множество целых чисел обозначается - Z. (да)

7ϵ N. (да)

Каждое рациональное число может быть представлено в виде бесконечной десятичной периодической дроби. (да)

⅓= 0,(3). (да)

8/9 >9/10. (да), т.к. 80/90> 81/90

– 3,192 > -3,193. (да)

1/7- можно представить в виде конечной десятичной дроби. (нет)

N ⊂ Z. (да)

Множество натуральных чисел обозначается - N. (да)

Q ⊂ N. (нет)

Всякое рациональное число можно представить в виде дроби ,

где m ϵ Z, n ϵ N. (да)

Множество целых чисел состоит из натуральных чисел и чисел им противоположных. (нет)

7/14 = 1/2 = 0,5. (да)

Целые и дробные числа составляют множество целых чисел. (нет)

Множество рациональных чисел обозначается – R.

37/5=7,4

Не существует числа, удовлетворяющего этому неравенству 1,3 < х < 1,4 . (нет), например 1,3<1,35<1,4

Запись М ⊂ Р, читают «Р подмножество М». (да)

-211 ∉ Z. (нет)

1/8 < 10/75 < 1/7 . (да)

4,7(28 оценок)

Ответ:

Msскрытность

03.08.2020

Пошаговое объяснение:

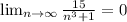$\lim_{n \to \infty} \frac{15}{n^3+1}=0$ . Докажем это.

По определению предела, для всякого положительного ε найдется номер N, что для всех номеров n, бОльших N, верно, что 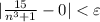$| \frac{15}{n^3+1}-0|< \varepsilon$ .

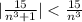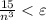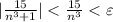Заметим, что $| \frac{15}{n^3+1}|< \frac{15}{n^3}$ для всякого натурального n. Тогда, если $\frac{15}{n^3}< \varepsilon$ , или (решая неравенство относительно n) $n \sqrt[3]{\frac{15}{\varepsilon}}$ , то, взяв в качестве N целую часть числа $\sqrt[3]{\frac{15}{\varepsilon}}$ , получим, что $| \frac{15}{n^3+1}|< \frac{15}{n^3} < \varepsilon$ . 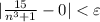Резюмируя: научились для всякого положительного ε находить номер N (в качестве N можно взять целую часть числа $\sqrt[3]{\frac{15}{\varepsilon}}$ ), что для всех номеров n, бОльших N, выполняется неравенство $| \frac{15}{n^3+1}-0|< \varepsilon$ . А это и значит, что предел равен нулю.

Интуитивно это можно объяснить так: увеличивая номер n, получаем все меньшее и меньшее число, причем оно всегда больше нуля, но его можно сделать очень маленьким.

Аналогично, докажем, что 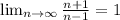$\lim_{n \to \infty} \frac{n+1}{n-1}=1$

По определению предела, для всякого положительного ε найдется номер N, что для всех номеров n, бОльших N, верно, что 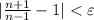$| \frac{n+1}{n-1}-1|< \varepsilon$ .

Заметим, что 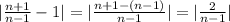$|\frac{n+1}{n-1}-1|=|\frac{n+1-(n-1)}{n-1}|=|\frac{2}{n-1}|$ . Тогда, если 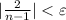$|\frac{2}{n-1}|< \varepsilon$ , или (решая неравенство относительно n) 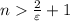$n \frac{2}{\varepsilon}+1$ , то, взяв в качестве N целую часть числа 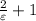$\frac{2}{\varepsilon}+1$ , получим, что 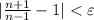$| \frac{n+1}{n-1}-1|< \varepsilon$ . Резюмируя: научились для всякого положительного ε находить номер N (в качестве N можно взять целую часть числа 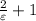$\frac{2}{\varepsilon}+1$ ), что для всех номеров n, бОльших N, выполняется неравенство 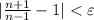$| \frac{n+1}{n-1}-1|< \varepsilon$ . А это и значит, что предел равен единице.