Задача
У трех девочек - Лизы, Маши, и Вики - шапочки разного цвета: красного, белого и синего. У кого какого цвета шапочка, если все записи неверные?
Запись:
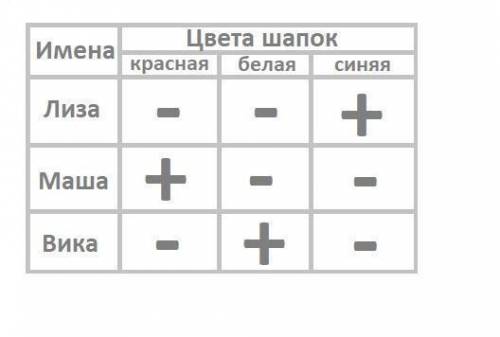
У Лизы белая шапочка. У Маши белая или синяя шапочка. У Вики красная шапочка.
Всего шапок три цвета: красная, белая, синяя. В условии говорится, что все утверждения неверны, а это значит, что все написанное в тексте противоположно сказанному. Следовательно, если у Лизы НЕ БЕЛАЯ шапка, значит либо КРАСНАЯ либо СИНЯЯ. У Маши НЕ БЕЛАЯ и НЕ СИНЯЯ шапка, а значит КРАСНАЯ. У Вики шапка НЕ КРАСНОГО цвета, а это значит либо СИНЯЯ либо БЕЛАЯ. Если у Лизы не может быть БЕЛОЙ шапки, а КРАСНАЯ на Маше, значит у Лизы шапка СИНЕГО цвета. Поскольку КРАСНАЯ шапка на Маше, а СИНЯЯ на Лизе, значит на Вике шапка БЕЛОГО цвета.
ответ: На Маше шапка красного цвета, на на Лизе синего, на Вике белого.
Рассуждение как просят в условии:
Начни рассуждать так; "Запись у Маши белая и синяя шапочка" неверна. Значит у Маши шапка КРАСНОГО цвета. Если запись"У Лизы белая шапочка" неверна, а шапка красного цвета на Маше, значит у Лизы шапка СИНЕГО цвета. Если шапка красного цвета на Маше, а синего на Лизе, значит на Вике шапка БЕЛОГО цвета.
ответ: На Маше шапка красного цвета, на на Лизе синего, на Вике белого.
ответ: утверждение доказано.
Пошаговое объяснение:
Возьмём сколь угодно малое положительное число ε. Мы докажем утверждение, если найдём такое число N, что при n>N будет выполняться неравенство /(n+b)/n-1/<ε. Данное неравенство равносильно двойному неравенству -ε<(n+b)/n-1<ε, или 1-ε<(n+b)/n<1+ε. Решением неравенства 1-ε<(n+b)/n является n>-b/ε, решением неравенства (n+b)/n<1+ε является n>b/ε. И если взять большее из чисел -b/ε и b/ε (обозначим его через с), то в качестве числа N можно взять либо само число с (если оно натуральное), либо ближайшее к нему и меньшее его натуральное число. Тогда числа N+1, N+2будут заведомо удовлетворять неравенству. Таким образом, по числу ε найдено соответствующее ему число N, поэтому утверждение доказано.