где a, b, c – стороны треугольника
S – площадь треугольника
Нам неизвестны ни стороны треугольника, ни его площадь. Обозначим катеты как х, тогда гипотенуза будет равна: x√2.
А площадь треугольника будет равна 0,5х².
Значит 2 = (2*0.5x²)/(x+x+x√2) = x²/(x(2+√2)) = x/(2+√2).
Сторона х = 4+2√2.
Таким образом, гипотенуза будет равна: с = (4+2√2)*√2 =
= 4+4√2 = 4(1+√2).
Можно выразить так: с ≈ 4(1+1,414214) ≈ 9,656854.
2) Так как центр вписанной окружности лежит на биссектрисе острого угла, то с = 2*r/(tg(45/2).
tg(45/2) можно взять из таблиц или выразить так:
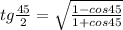 .
.
Результат тот же: с ≈ 9,656854.
3х+7>7x-9;
x-3>-3x+1;
4x<16;
4x>4;
x<4;
x>1;
ответ: x∈(1;4).