Из вершины В параллелограмма ABCD проведем высоту ВН к стороне AD. Рассмотрим треугольник АВН: угол АНВ = 90 градусов (так как ВН - высота, перпендикуляр), АВ = 6 см (по условию) - гипотенуза (так как лежит против угла 90 градусов), угол ВАН = угол А = 30 градусов (по условию). Катет ВН лежит против угла равного 30 градусов, поэтому:
ВН = АВ/2 (свойство прямоугольного треугольника);
ВН = 6/2 = 3 (см).
Площадь параллелограмма находится по формуле:
S = a*h,
где а - сторона параллелограмма, h - высота, опущенная на сторону а.
S = AD*BH;
S = 10*3 = 30 (см квадратных).
ответ: S = 30 см квадратных.
7/Задание № 7:
На двух параллельных прямых отметили семь точек: три на одной и четыре на другой. Сколько существует четырёхугольников с вершинами в этих точках?
РЕШЕНИЕ: Понятно, что две точки нужно выбрать с одной прямой, а две - с другой, иначе три точки будут лежать на одной прямой и в качестве фигуры получится треугольник.
Выбрать две точки с первой прямой: 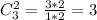
Выбрать две точки со второй прямой: 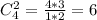
Так как выбор независим, то выбрать 4 точки можно то есть имеется 18 четырёхугольников.
ОТВЕТ: 18 четырёхугольников