Відповідь:
400кг
Покрокове пояснення:
2,5т=2500кг(так удобнее)
2500:100·16=400кг
Пошаговое объяснение:
сначала упростим общий вид членов ряда
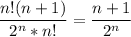
(это можно сделать, пользуясь свойствами пределов - получим равнозначный ряд)
теперь применим ризнак Даламбера
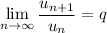
при q < 1 - ряд сходится, q > 1 - ряд расходится, q = 1 - неопределенность (дополнительные исследования)
у нас
при q < 1 - ряд сходится, q > 1 - ряд расходится, q = 1 - получаем неопределенность (дополнительные исследования)
у нас
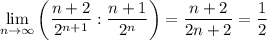
q < 1 - ряд сходится
( можно было и сразу "в лоб" применять признак Даламбера не упрощая формулу - результат был бы тот же...)
Пошаговое объяснение:
сначала упростим общий вид членов ряда
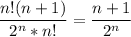
(это можно сделать, пользуясь свойствами пределов - получим равнозначный ряд)
теперь применим ризнак Даламбера
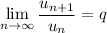
при q < 1 - ряд сходится, q > 1 - ряд расходится, q = 1 - неопределенность (дополнительные исследования)
у нас
при q < 1 - ряд сходится, q > 1 - ряд расходится, q = 1 - получаем неопределенность (дополнительные исследования)
у нас
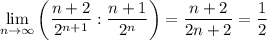
q < 1 - ряд сходится
( можно было и сразу "в лоб" применять признак Даламбера не упрощая формулу - результат был бы тот же...)
400 кг
Пошаговое объяснение:
2,5т-100%
Х - 16%
Х=2500*16/100=400кг сушених яблок получится из 2,5т свежих яблок