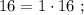
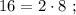
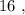т.е.: 
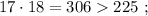
каждое – будет, очевидно, больше чем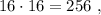 
т.е. больше 
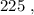а значит, при выборе минимальных чисел в виде 
и – подобрать остальные числа невозможно.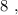
т.е.: 
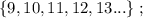
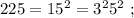
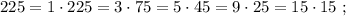
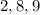и 
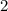и 
и 
Вася никаких чисел добавить не мог бы, поскольку тогда минимальные числа стали бы другими, и их произведение уже не было бы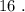 
и никаких натуральных чисел нет. и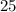 
Вася тоже никаких чисел добавить не мог бы, поскольку тогда максимальные числа стали бы другими, и их произведение уже не было бы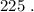 
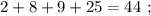
Пошаговое объяснение:
Требуется вычислить площадь, заключенную между параболой y=x^2-2 и прямой y=2x+1.
Найдем точки пересечения параболы и прямой:
\[\left\{ \begin{array}{l}y = {x^2} - 2\\y = 2x + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x + 1 = {x^2} - 2\\y = 2x + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x + 1 - {x^2} + 2 = 0\\y = 2x + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - {x^2} + 2x + 3 = 0\\y = 2x + 1\end{array} \right.\]% MathType!End!2!1!
- {x^2} + 2x + 3=0
Найдем дискриминант квадратного уравнения:
D = {b^2} - 4a = {2^2} - 4( - 1)*3 = 4 + 12 = 16
{x_{1,2}} = \frac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}
{x_1} = \frac{{ - 2 - \sqrt {16} }}{{2*( - 1)}} = \frac{{ - 2 - 4}}{{ - 2}} = \frac{{ - 6}}{{ - 2}} = 3
{x_2} = \frac{{ - 2 + \sqrt {16} }}{{2*( -1)}} = \frac{{-2+ 4}}{{- 2}} = \frac{2}{{-2}} =-1
Подставим x в уравнение:
y₁=7; y₂=-1
Получаем две точки пересечения : (3;7) и (-1;-1)
Пределы интегрирования a=-1, b=3. Площадь фигуры равняется:
S = \int\limits_{- 1}^3 {(2x + 1) - ({x^2} - 2)dx =} \int\limits_{-1}^3 (-{x^2} + 2x + 3)dx =
= - \int\limits_{- 1}^3 {{x^2}dx + } 2\int\limits_{- 1}^3 {x *dx}+3\int\limits_{- 1}^3 {1 *dx}=- \left. {\frac{{{x^3}}}{3}} \right|_{- 1}^3 + 2\left. {\frac{{{x^2}}}{2}} \right|_{- 1}^3+3\left. {\frac{x}{1}} \right|_{ - 1}^3
F(3) =- \frac{{{3^3}}}{3} + {3^2} + 3*3 = 9
F( - 1) =- \frac(- 1)}^3}}}{3} + {(-1)^2} + (- 1)*3 =- \frac{5}{3}
F(3) - F( - 1) = 9 - (- \frac{5}{3}) = \frac{{32}}{3} \approx 10,7
Графики прилагаются.