В решении.
Пошаговое объяснение:
В квадратной комнате стелили линолеум. Причем было 2 квадратных куска, сторона одного из них была в 4 раза больше стороны другого. Если положить эти куски в противоположных углах комнаты, то площадь, накрытая обоими кусками, составила 16 кв.м, если же положить их в соседние углы (вдоль одной стороны), то 32 кв.м. Какова длина стороны комнаты?
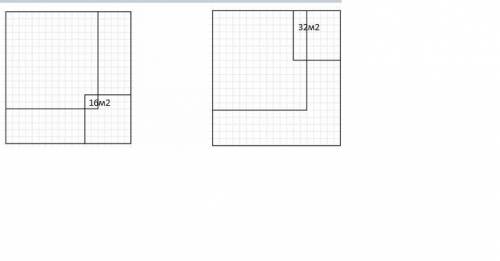
В первом случае пересечением кусков линолеума является квадрат площади 16 м² (рис. слева), значит, длина стороны этого квадрата равна 4 м.
Во втором случае пересечением кусков линолеума является прямоугольник, одна сторона которого также равна 4 м (рис. справа). Следовательно, другая сторона этого прямоугольника равна 32 : 4 = 8 (м), это длина стороны меньшего куска линолеума.
Значит, сторона большего куска линолеума имеет длину 8*4 = 32 (м) (по условию задачи в 4 раза больше стороны меньшего куска).
Так как стороны кусков линолеума накладываются друг на друга на 4 м, то длина стороны комнаты равна 8 + 32 – 4 = 36 (м).
Рисунки к задаче схематичные, размеры по условию задачи и по клеткам не совпадают.
Будем считать, что дана функция у = (x²+8) / (x+1).
Находим её производную.
y' = 2x*(x + 1) - 1*(x² + 8) / (x + 1)² = (x² + 2x - 8) / ((x + 1)²).
Для определения критических точек приравняем её нулю (достаточно числитель, исключив х = -1).
x² + 2x - 8 = 0,
D = (2²-4*1*(-8)) = 36, √D = +-6.
x1 = (-2 - 6)/(2*1) = -4, x2 = (-2 + 6) / (2*1) = 2.
На заданном промежутке критическая точка х = 2.
Определим её характер по значениям производной левее и правее этой точки.
х = 1 2 3
y' = -1,25 0 0,4375.
Как видим, это минимум функции (переход производной с - на +).
Значение функции в точке экстремума равно:
у = (2² + 8) / (2 + 1) = 12/3 = 4.
Чтобы найти наибольшее значение функции на заданном промежутке, определим её значения на концах промежутка.
х = 0, у = 8,
х = 3, у = 4,25.
ответ: наибольшее значение функции у = 8,
наименьшее значение функции у = 4.