| - 0,63 | : | x | = | - 0,9 | ;
| - 0,63 : x | = | - 0,9 | ;
Модуль раскрывается со знаком плюс и минус. Получим 2 уравнения: - 0.63 / x = - 0.9 и - ( - 0.63 / x ) = - 0.9.
Решим их по отдельности:
1 ) - 0,63 / x = - 0.9 ;
Правую и левую часть выражения умножим на x, тогда получим:
- 0,63 / x = - 0.9 ;
-0.63 / x * x = - 0.9 * x ;
- 0.63 = - 0.9 * x ;
x = - 0.63 / ( - 0.9 ) ;
x = 0.63 / 0.9 ;
x = 0.7 ;
2 ) - ( - 0.63 / x ) = - 0.9 ;
Раскрываем скобки. Так как, перед скобками стоит знак минус, то при ее раскрытии, знаки значений меняются на противоположный знак. То есть получаем:
0.63 / x = - 0.9 ;
x = - 0.7 ;
ответ: х = -0,7 и х = - 0,7.
Пошаговое объяснение:
Пошаговое объяснение:
1) По формулам,которые я привел ниже
C4 8 = 8!/(4! * 4!) = (1*2*3*4*5*6*7*8)/(1*2*3*4 * 1*2*3*4) = (5*6*7*8)/(1*2*3*4) = (2*5*7)/1 = 70
Здесь воспользуемся объединенной ф-лой(привел ниже)
A4 8 = 70 * 4! = 40 * 1*2*3*4 = 960
2) С3 5 = 5!/(2! * 3!) = (1*2*3*4*5)/(1*2 * 1*2*3) = 10
А3 5 = 10 * 3! = 10*1*2*3 = 60
3) С2 100 = 100!/(98! * 2!) = (98! * 99 * 100)/(98! * 1*2) = (99*100)/2 = 4950
А2 100 = 4950 * 2! = 4950 * 2 = 9900
4) С2 17 = 17!/(15! * 2!) = (15! * 16*17)/(15! * 1*2) = (16*17)/2 = 136
А2 17 = 136 * 2! = 136* 1*2 = 272
5)С3 10 = 10!/(7! * 3!) = (7! * 8*9*10)/(7! * 1*2*3) = (8*9*10)/(1*2*3) = 120
А3 10 = 120 * 3! = 120 * 1*2*3 = 720
А3 10/С3 10 = 720/120 = 6
6) А6 8 = 8!/2! = (1*2*...*7*8)/(1*2) = 3*4*5*6*7*8 = 20160
А2 10 = 10!/8! = (8! *9*10)/8! = 90
А6 8 / А2 10 = 20160/90 = 224
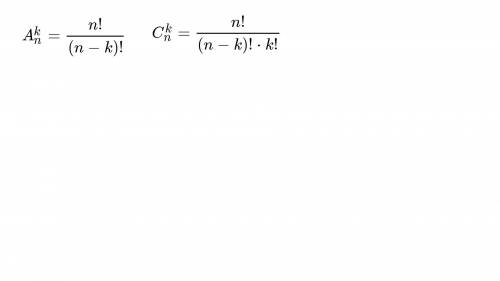
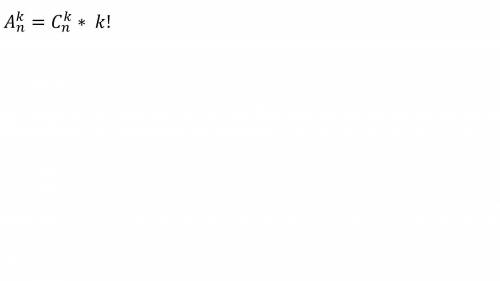
ответ:22
Пошаговое объяснение: Периметр это сумма всех сторон. Так как в прямоугольнике противолежащие стороны равны P=7+4+7+4=22см