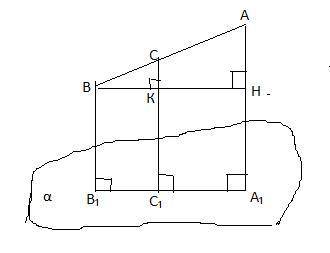
Даны плоскость α и не пересекающий данную плоскость отрезок AB. На этом отрезке взята точка C так, что AC : CB = 3 : 2. Найдите расстояние (cm) от точки C до плоскости α, если расстояния из концов отрезка AB до плоскости равны AA1=18 cm и BB1=13 cm.
Пошаговое объяснение:
Т.к. AC : CB = 3 : 2 ,то АВ составляет 5 частей, ВС-две части отрезка АВ.
Т.к. в задаче идет речь о расстояниях , то АА₁⊥α, СС₁⊥α , ВВ₁⊥α ⇒ АА₁║СС₁║ВВ₁.
Пусть ВН⊥АА₁ ⇒АН=18-13=5 (см) . Отрезок СС₁=СК+КС₁ .
ΔАВН подобен ΔСВК по 2 углам :∠В -общий,∠ВКС=∠ВНА=90° ⇒ сходственные стороны пропорциональны :
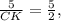 СК=2 см.
СК=2 см.
СС₁=2+13=15 (см)
Пошаговое объяснение:
1. нужно взять два прямоугольных треугольника таких, чтобы один из катетов был равен половине гипотенузы, например а = 0,5с (с - гипотенуза)
сложить эти треугольники катетами b "друг к дружке". получим равносторонний треугольник со сторонами равными с
и площадью S = (c²√3)/4
2. извините, не соображу наверное опять же прямоугольный треугольник, только складывать надо гипотенузами друг к другу
3. вероятностью наступления события в некотором испытании называют отношение Р(А) = m/n
m - общее число всех равновозможных, элементарных исходов этого испытания, которые образуют полную группу событий,
n - количество элементарных исходов, благоприятствующих событию A
теперь, что у нас.
в результате броска кубика может появиться n = 6 элементарных равновозможных исходов, образующих полную группу - 6 сторон и может выпасть одна из них с одинаковой вероятностью
а событию выпадения любой стороны благоприятствует единственный исход (выпадение этой стороны).
В₁ - выпадение 1, В₂ - двойки , и т.д.
и вот что у нас получается
Р(В₁) = Р(В₂) = Р(В₆) = 1/6