Для начала вспомним, что тупой угол - это угол с градусной мерой больше 90° и меньше 180°. Из одной точки можно пустить три луча, которые между собой образуют 3 тупых угла. Пустим 4-й луч вблизи одного из трёх лучей, у нас добавится дополнительно 2 тупых угла. 5-й луч пустим вблизи второго из числа первых трёх, дополнительно образуются 3 тупых угла. Наконец, пускаем 6-й луч вблизи третьего, получив дополнительно 4 тупых угла. У нас будет получаться как бы три пучка близко расположенных лучей в каждом пучке. Считаем сколько получилось тупых углов после добаления к первым трём лучам ещё трёх лучей. 3 луча было, плюс 2, плюс 3 и плюс 4, всего 12 лучей. Итак, для 3-х лучей - 3 тупых угла; для 6 лучей - 12 тупых углов. Рассуждаем аналогично, добавляя по очереди ещё 3 луча. Добавятся сначало 4 угла, затем 5 и, наконец, 6; т.е. всего добавится 15 тупых углов. А всего для 9 лучей будет 27 тупых углов. Точно также, считая для 12 лучей, получим дополнительно 6+7+8 = 21 тупых угла, а всего - 48. Можно было бы и далее продолжать таким но мы замечаем закономерность. Пусть а1 = 3 - это первый член последовательности. Используя предыдущее значение (рекуррентно), можно вычислить следующее значение по формуле: , где n - число лучей кратное 3. Пробуем вычислить по этой формуле:
Итак, для 18 лучей возможно максимум 108 тупых угла.
(1) питнадцать и две целых одна седьмая 14+7/7 и 2+1/7 (2) тридцать четыре и пять целых три восьмых 33+8/8 и 5+3/8 (3) сорок пять целых пять одиннадцатых и девять 45+5/11 и 8+11/11 (4) тридцать шесть целых семь двенадцатых и одиннадцать 36+7/12 и 10+12/12 (5) сто и одна целая пять девяносто девятых 99+99/99 и 0+5/99 (6) девяносто шесть и тринадцать целых двадцать пять сорок шестых 95+46/46 и 13+5/46 приведите дроби к наименьшему общему знаменателю:
(1) одна четвёртых,семь петнадцатых и пять шестых 1/4=15/60 7/15=28/60 5/6=50/60 (2) тринадцать четырнадцатых,пять двадцать первых и две третьих 13/14=39/42 5/21=10/42 2/3=26/42 (3) две петнадцатых,пять двенадцатых и три четвёртых 2/15=8/60 5/12=25/60 3/4=45/60 (4) три четвёртых,одиннадцать восемнадцатых,семь тридцать шестых и одна десятая 3/4=135/180 11/18=110/180 7/36=35/180 1/10=18/180
(5)семь петнадцатых,девятнадцать двадцать первых,одна вторых и одиннадцать четырнадцатых 7/15=98/210 19/21=190/210 1/2=105/210 11/14=165/210 (6)восемь девятых,девятнадцать тридцатых,четырнадцать петнадцатых и 8/9=240/270 19/30=171/270 14/15=252/270 11/27=110/270
Для начала вспомним, что тупой угол - это угол с градусной мерой больше 90° и меньше 180°. Из одной точки можно пустить три луча, которые между собой образуют 3 тупых угла.
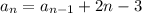, где n - число лучей кратное 3.
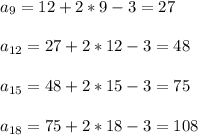
Пустим 4-й луч вблизи одного из трёх лучей, у нас добавится дополнительно 2 тупых угла. 5-й луч пустим вблизи второго из числа первых трёх, дополнительно образуются 3 тупых угла. Наконец, пускаем 6-й луч вблизи третьего, получив дополнительно 4 тупых угла. У нас будет получаться как бы три пучка близко расположенных лучей в каждом пучке.
Считаем сколько получилось тупых углов после добаления к первым трём лучам ещё трёх лучей. 3 луча было, плюс 2, плюс 3 и плюс 4, всего 12 лучей.
Итак, для 3-х лучей - 3 тупых угла; для 6 лучей - 12 тупых углов.
Рассуждаем аналогично, добавляя по очереди ещё 3 луча. Добавятся сначало 4 угла, затем 5 и, наконец, 6; т.е. всего добавится 15 тупых углов. А всего для 9 лучей будет 27 тупых углов.
Точно также, считая для 12 лучей, получим дополнительно 6+7+8 = 21 тупых угла, а всего - 48.
Можно было бы и далее продолжать таким но мы замечаем закономерность.
Пусть а1 = 3 - это первый член последовательности. Используя предыдущее значение (рекуррентно), можно вычислить следующее значение по формуле:
Пробуем вычислить по этой формуле:
Итак, для 18 лучей возможно максимум 108 тупых угла.