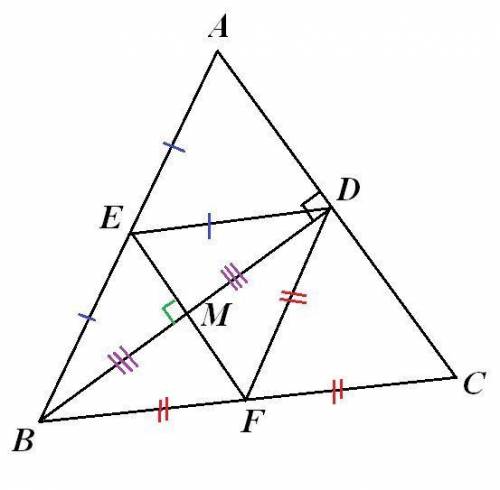
Мой чертеж - во вложении.
1) Докажем сначала пункт Б).
Т.к. по условию Е-середина АВ, F-середина ВС, то EF-средняя линия ΔАВС. ⇒ FE║AC.
Т.к. BD-высота, то BD⊥AC ⇒ BD⊥FE (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и второй прямой). Доказано.
2) Докажем равенство углов EBF и EDF. Пусть BD и EF пересекаются в точке М.
По теореме Фалеса: т.к. FE║AC и F-середина ВС, то М-середина BD.
⇒ в Δ BED EМ-это медиана и высота. ⇒ Δ BED-равнобедренный ⇒ BE=ED.
Аналогично доказывается, что Δ BFD-равнобедренный ⇒ BF=FD.
Рассмотрим Δ EBF и Δ EDF. По доказанному выше они равны по трём сторонам (BE=ED, BF=FD, EF-общая). ⇒∠EBF=∠EDF. Доказано.
Длина окружности
Формула длины окружности радиуса r или диаметра d = 2r имеет вид:
или
где \pi \approx 3,14 – число «пи».
Примеры решения задач
ПРИМЕР 1
Задание Найти длину окружности диаметра 1,5 см.
Решение Для нахождения длины заданной окружности воспользуемся формулой l = \pi d. Подставляя в неё значение d = 1,5 см, получим
l = 1,5 \cdot \pi = 1,5 \pi (см)
Учитывая, что \pi \approx 3,14 окончательно имеем:
l = 1,5 \pi \approx 1,5 \cdot 3,14 = 4,71 (см)
ответ Длина окружности равна l = 1,5 \pi см или l \approx 4,71 см.
Контрольные работы на заказ
Решаем контрольные по всем предметам. 10 лет опыт! Цена от 100 руб, срок от 1 дня!
Онлайн заказЦены и сроки
Нужно решить задачи?
Решаем задачи любой сложности от 1 дня! Недорого и точно в срок. Заказывай!
Наши услугиБыстрый заказ
ПРИМЕР 2
Задание Найти длину окружности, вписанную в правильный треугольник со стороною 4 \sqrt{3} см.
Решение Сделаем рисунок (рис. 2).
По условию a = 4 \sqrt{3} см. Сторона правильного треугольника связана с радиусом вписанной в него окружности следующим соотношением:
\[ r=\frac{a}{2 \sqrt{3}} \]
Подставляя в последнее равенство заданное значение стороны правильного треугольника a = 4 \sqrt{3} см, найдем радиус вписанной окружности:
(см)
Длину окружности найдем по формуле:
\[ l=2 \pi r \]
Подставляя в неё найденное значение радиуса, будем иметь:
l = 2 \cdot 2 \cdot \pi = 4 \pi (см)
Если так же подставить \pi \approx 3,14, окончательно получим:
l = 4 \pi \approx 4 \cdot 3,14 = 12,56 (см)
ответ l = 4 \pi см или l \approx 12,56 см.
Пошаговое объяснение: