По условию задания составим уравнение расстояния произвольной точки М(х; у) от точки P(1; -1) в 2 раза меньшего, чем от точки М до прямой х = 4.
√((x-1)² + (y + 1)²) = |4 - x)|/2.
Модуль в правой части взят, чтобы длина не была отрицательной для точек, расположенных левее оси Оу.
Возведём обе части в квадрат.
x² - 2x + 1 + (y + 1)² = (16 - 8x + x²)/4,
4x² - 8x + 4 + 4(y + 1)² = 16 - 8x + x²,
Приведём подобные: 3x² + 4(y + 1)² = 12.
Разделим обе части на 12.
(3x²/12) + (4(y + 1)²)/12 = 1. Приведём к каноническому виду.
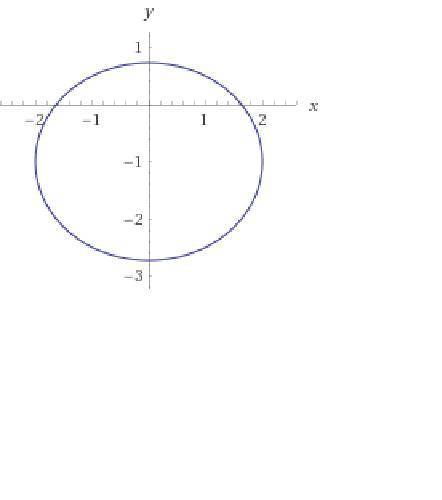
(x²/2²) + ((y + 1)²)/(√3)²) = 1.
Получено искомое уравнение. Это уравнение эллипса.
Центр её расположен в точке (0; -15).
Полуоси: действительная равна а =2, мнимая b = √3.
Найдем координаты ее фокусов: F1(-c;0) и F2(c;0), где c - половина расстояния между фокусами
Определим параметр c: c² = a² - b² = 4 - 3 = 1 .
c = √1 = 1.
Тогда эксцентриситет будет равен: е = с/а = 1/2 .
х + у + z = 198
x : y = 2 : 7
y : z = 4 : 9
7 : 4 = 1,75 - доп. множ. ко второй пропорции
у : z = (4·1,75) : (9·1,75) = 7 : 15,75
х : у : z = 2 : 7 : 15,75
Пусть k - коэффициент пропорциональности, тогда х = 2k, y = 7k, z = 15,75k. Уравнение:
2k + 7k + 15,75k = 198
24,75k = 198
k = 198 : 24,75
k = 8
x = 2 · 8 = 16
у = 7 · 8 = 56
z = 15,75 · 8 = 126
Вiдповiдь: 16, 56 i 126.
Проверка:
х + у + z = 16 + 56 + 126 = 198 - сумма трёх чисел
х : у = 2 : 7 = 16 : 56 = 0,(285714) - отношение х к у
у : z = 4 : 9 = 56 : 126 = 0,(4) - отношение у к z