frac{\pi }{2} +2\pi n,~n\in\mathbb {Z} } , \pi +2\pi k, ~k\in\mathbb {Z} .
Пошаговое объяснение:
\sqrt{1+cosx} =sin x.
1+cosx
=sinx.
Возведем обе части уравнения в квадрат при условии
sinx\geq 0.sinx≥0.
\begin{gathered}1+cosx= sin^{2} x;\\1+cosx=1-cos^{2} x;\\cos^{2} x+cosx=0;\\cosx(cosx+1)=0 ;\\\left [ \begin{array}{lcl} {{cosx=0,} \\ {cosx=-1;}} \end{array} \right.\Leftrightarrow \left [ \begin{array}{lcl} {{x=\frac{\pi }{2} +\pi n,~n\in\mathbb {Z} } \\ {x=\pi +2\pi k, ~k\in\mathbb {Z}}} \end{array} \right.\end{gathered}
Учтем условие , что sinx\geq 0sinx≥0 . Тогда получим
\begin{gathered}\left [ \begin{array}{lcl} {{x=\frac{\pi }{2} +2\pi n,~n\in\mathbb {Z} } \\ {x=\pi +2\pi k, ~k\in\mathbb {Z}}} \end{array} \right.\end{gathered}
Если треугольник равнобедренный, то углы при основании равны.
В этой задаче есть расстановки углов:
1-ый
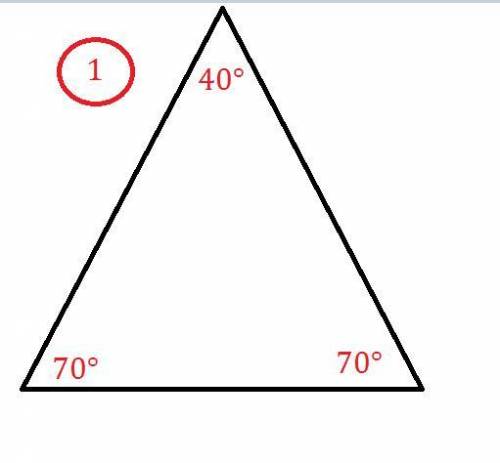
Если угол в 70° лежит при основании треугольника (Картинка №1).
Тогда, второй угол при основании тоже будет 70°. А третий угол будет равен:
180°-(70°+70°)=180°-140°=40°-по теореме о сумме углов в треугольнике.
2-ой
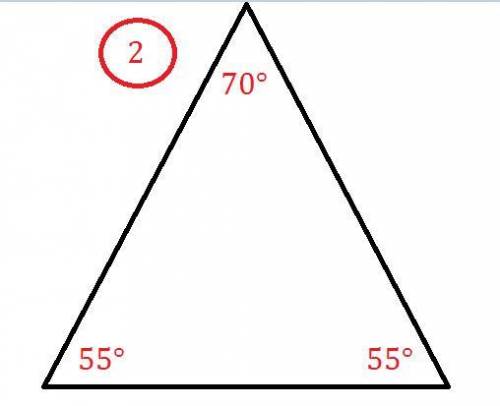
Если угол в 70° лежит НЕ при основании треугольника (Картинка №2).
Тогда, каждый из 2-ух углов, которые лежат при основании будут равны:
(180°-70°):2=110°:2=55°-по теореме о сумме углов в треугольнике.
2) 50:20=2,5 см - ширина