1) Точка А = 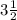 , а точка В =
, а точка В = 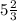 ⇒ расстояние между ними равно В - А
⇒ расстояние между ними равно В - А
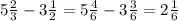
2) Натуральными числами называют целые числа, использующиеся при счёте
Нужно чтобы числа соответствовали неравенству 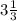 < x < 7
< x < 7
Т.к. 3<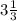 ⇒ нам нужна сумма чисел от 4 до 7, то есть 4 ≤ x < 7
⇒ нам нужна сумма чисел от 4 до 7, то есть 4 ≤ x < 7
4+5+6 = 15
3) Среднее арифметическое находится сложением данных чисел и делением их на их количество
а) 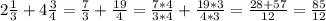
б) 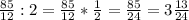
4) Действуем аналогично как в 3 задании
а) 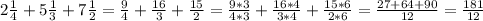
б) 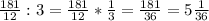
5) Действуем аналогично как в 2 задании
Нужно чтобы числа соответствовали неравенству 1 < x < 47,5
Т.к. 47,5 < 48 ⇒ нам нужно посчитать количество целых чисел от 1 до 47, то есть 1 < x ≤ 47
Их 46
Пусть основание - треугольник ABC со сторонами AB=25дм, BC=29дм, AC=36дм. Найдем его площадь. S_ABC=1/2*AB*AC*sin∠A. Найдем cos∠A по теореме косинусов: cos∠A = (AB^2+AC^2-BC^2)/(2*AB*AC)=(25^2+36^2-29^2)/(2*25*36) = 0.6. Отсюда sin∠A = √(1-(cos∠A)^2)=0.8.
Тогда S_ABC = 1/2 * 25 * 36 * 0.8 дм^2 = 360 дм^2.
Площадь боковой поверхности равна разности площади всей поверхности и суммы площадей оснований призмы. То есть Sбок=1620 - 2*360 дм^2 = 900 дм^2
С другой стороны, Sбок = P*H, где H-высота призмы, P = AB+BC+AC - периметр основания. P = 25+29+36 дм = 90 дм. Отсюда H = Sбок/P=900/90 дм = 10 дм.
Пошаговое объяснение: