ответ:50 и 40 градусов
Пошагово: пусть один угол х то второй х*4/5, где х+4/5х=90градусов,отсюда х=50градусов, второй 90-50=40
Если dydx=f(x)dydx=f(x), то yy - это функция, производная которой равна f(x)f(x). Такая функция называется первообразной от функции f(x)f(x) или неопределенным интегралом от f(x)f(x) и обозначается f(x)dxf(x)dx. Аналогично, если y=∫f(u)duy=∫f(u)du, то dydu=f(u)dydu=f(u). Поскольку производная константы равна нулю, все неопределенные интегралы от одной функции отличаются на константу.
Процедура нахождения значения интеграла называется интегрированием.
Далее приняты следующие обозначения: u,v,wu,v,w - функции от переменной xx;
a,b,p,q,na,b,p,q,n - произвольные константы, ограниченные, если об этом сказано;
e=2,71828...e=2,71828... - основание натурального логарифма;
lnulnu обозначает натуральный логарифм от uu, где u>0u>0 (для обобщения формул на случай u>0u>0необходимо заменить lnulnu на ln|u|ln|u|);
все углы считаются в радианах;
все константы интегрирования опущены, но предполагается, что они существуют.
ИССЛЕДОВАНИЕ
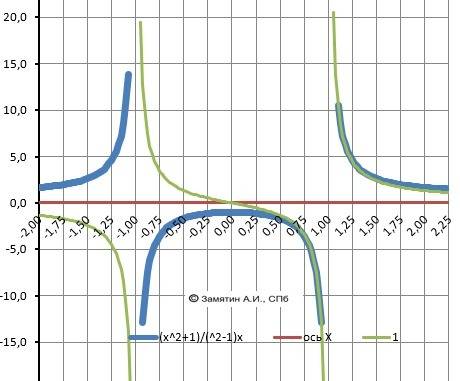
1.Область определения D(x).
x²- 1 = (x+1)(x-1) ≠ 0, x≠ +/-1. Два разрыва.
Х∈(-∞;-1)∪(-1;1)∪(1;+∞).
2. Вертикальные асимптоты - две: Х=-1, Х=1.
3. Пересечение с осью Х. Y=0 - нет.
3. Пересечение с осью У. У(0) = -1.
4. Поведение на бесконечности. Сокращаем на х² - числитель и знаменатель.
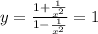
limY(-∞) = (1+0)/(1-0) = 1. Справа Y=1. limY(+∞) = 1.
Горизонтальная асимптота - Y= 1.
5. Исследование на чётность.Y(-x) = Y(x).
Функция чётная.
6. Производная функции.
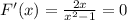
Корень при Х=0.
7. Локальные экстремумы.
Максимум - Y(0) = -1 . Минимума - нет.
8. Интервалы монотонности.
Возрастает - Х∈[-∞;-1)∪(1;0], убывает - X∈[0;1)∪(1;+∞)
9. Вторая производная - Y"(x). Анализируем первую производную.
Максимума Y'(x) - нет - точек перегиба НА ГРАФИКЕ - нет.
9. Выпуклая “горка» Х∈(-1;1), Вогнутая – «ложка» Х∈(-∞;-1)∪(1;+∞).
10. Поведение в точках разрыва.
lim(-1-)Y(x) = +∞,lim(-1+)Y(x) = -∞,lim(1-)Y(x) =-∞,lim(1+)Y(x) = +∞,
11. График в приложении.
т.к. прямые перпендикулярны угол между ними равен 90°. Тогда составим уравнение:
ABD=5/4 × DBC
5/4 × DBC + DBC = 90
5DBC+4DBC=360
9DBC=360
DBC=40°
ABD=5/4 × 40=50°