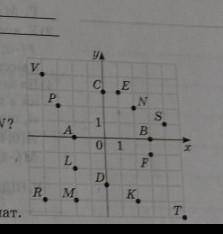
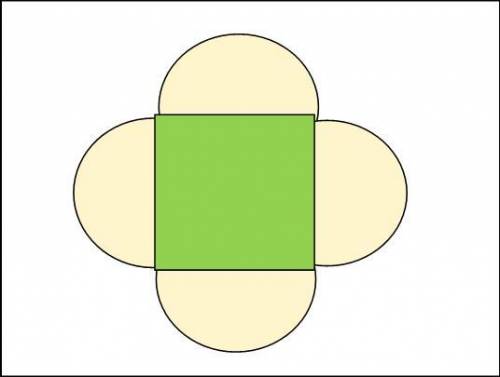
Пусть 
(м) - сторона квадрата, тогда
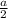(м) - длина радиуса полукругов
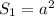(м²) - площадь квадрата
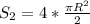(м²) - площадь 4-х полукругов через радиус
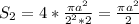(м²) - площадь 4-х полукругов через /
Теперь выразим площадь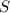 
всей клумбы:
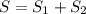
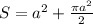
По условию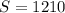 
м² и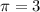 
, поставим в последнее уравнение и найдем .
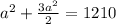
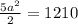
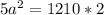
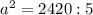
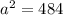
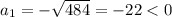
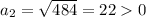
ответ первый: 22 м - длина стороны квадрата.
22 : 2 = 11
ответ второй: 11 м - длина радиуса полукругов.
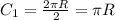длина одного полукруга.
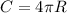длина 4-х полукругов, она же и есть длина декоративного забора.
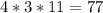
ответ третий: 77 м - длина декоративного забора.
Жёлтым цветом все точки.
Пошаговое объяснение:
Я такой задачи за свои 5-9 классы не встречал :) И вот что вышло :
Система имеет вид :
x^2 + y^2
4 - уравнение окружности, с радиусом большим, либо равным 2 => первая область определения двух переменных, при которой они не могут быть равными значениям внутри окружности.
y - 2x < 0 ; y < 2x - (немного непросто понять) означает, что значения переменных не могут удовлетворять прямым y = 2x и y > 2x => прямая y = 2x - означает, что значение слева прямой и самой прямой не удовлетворяют условию => чертим графики :
ответом служат все точки координатной плоскости, находящиеся правее от прямой y = 2x (желтым цветом намалякал), но не лежащие внутри окружности (но на самой могут лежать).
Областью определения является сама система :)