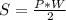, где 
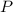— периметр основания, а 
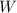— апофема. 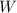в условии дана (6 см), осталось найти периметр основания 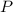. Напомню, что периметр — это сумма длин всех сторон. В основании правильной четырехугольной пирамиды лежит квадрат. У квадрата все стороны равны. Поэтому его периметр найдем по формуле 
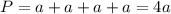, где 
— сторона квадрата. Из условия ясно, что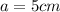 
, отсюда 
.
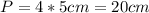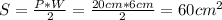. Готово! 
243
14 17.3571428
-103
98
-50
42
-80
70
-100
98
-20
14
-60
56
-40
28
-120
112
8
6372 12
60 531
-37
36
-12
12
0
10914 34
102 321
71
68
-34
34
0
3912 12
36 326
-31
24
-72
72
0
6404 15
60 427
-40
30
-105
105
0
10104 12
96 842
-50
48
-24
24
0
394515
30 263
-94
90
-45
45
0
7 96515
75 531
-46
45
-15
15
0
Пошаговое объяснение:
Долго((