Имеем дело с однородной СЛАУ, у которой кол-во неизвестных больше кол-ва уравнений, значит, имеем нетривиальные решения.
Приведем матрицу к ступенчатому виду:
![\left[\begin{array}{cccc}-4&1&2&1\\7&4&1&0\\1&2&5&0\end{array}\right]](/tpl/images/1148/9647/1ba93.png)
Меняем 1 и 3 строки:
![\left[\begin{array}{cccc}1&2&5&0\\7&4&1&0\\-4&1&2&1\end{array}\right]](/tpl/images/1148/9647/483ee.png)
Вычитаем из второй строки первую, умноженную на 7:
![\left[\begin{array}{cccc}1&2&5&0\\0&-10&-34&0\\-4&1&2&1\end{array}\right]](/tpl/images/1148/9647/91dae.png)
Делим на -2 вторую строку и прибавляем к 3 строке первую, умноженную на 4:
![\left[\begin{array}{cccc}1&2&5&0\\0&5&17&0\\0&9&22&1\end{array}\right]](/tpl/images/1148/9647/64e50.png)
Вычитаем из 3 строки вторую:
![\left[\begin{array}{cccc}1&2&5&0\\0&5&17&0\\0&4&5&1\end{array}\right]](/tpl/images/1148/9647/7a4f0.png)
Вычитаем из 2 строки третью:
![\left[\begin{array}{cccc}1&2&5&0\\0&1&12&-1\\0&4&5&1\end{array}\right]](/tpl/images/1148/9647/149c0.png)
Вычитаем из 3 строки вторую, умноженную на 4:
![\left[\begin{array}{cccc}1&2&5&0\\0&1&12&-1\\0&0&-43&5\end{array}\right]](/tpl/images/1148/9647/7a475.png)
Ранг равен трем, откуда количество свободных переменных равно 4 - 3 = 1. Пусть D - свободная переменная. Тогда
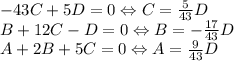
Значит,
![\left[\begin{array}{c}A\\B\\C\\D\end{array}\right] = D\left[\begin{array}{c}\frac{9}{43} \\{-\frac{17}{43}}\\\frac{5}{43}\\1\end{array}\right] = \tilde{D}\left[\begin{array}{c}9\\-17\\5\\43\end{array}\right]](/tpl/images/1148/9647/c00d2.png)
ответ: векторы вида ![\tilde{D}\left[\begin{array}{c}9\\-17\\5\\43\end{array}\right]](/tpl/images/1148/9647/1e9f9.png) , при
, при  .
.
Пошаговое объяснение:
Рисунок с расчётом к задаче в приложении.
ОТВЕТЫ
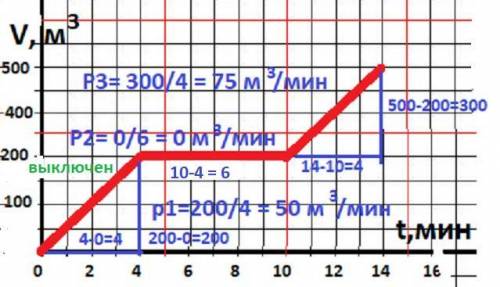
1) Найти время остановки. Выключен насос - объём воды не изменяется -горизонтальный участок графика - прямая на уровне 200 м³ проходит от t₁ = 4 t₂ = 10.
Т = 10 - 4 = 6 мин - время остановки - ответ.
2) Производительность работы до остановки.
По формуле РАБОТЫ: A =P*t. В нашей задаче работа это V - объём воды. Производительность работы находим по формуле: p = ΔV/Δt = (V₂ - V₁)/(t₂ - t₁).
р1 = (200 - 0) : (4-0) = 200/4 = 50 м³/мин = р1 - до остановки - ответ.
3) Производительность после остановки.
р2 = (500-200)/(14 - 10) = 300/4 = 75 м³/мин = р3 - после остановки - ответ.ₙ
Пошаговое объяснение:
x - 154 = 43
x = 154 + 43
x = 197