![4. [4б.] На рисунке изображен график движения пешехода из пункта Ав пункт В. Используя график, ответ](/tpl/images/4469/1416/30228.jpg)
Дано уравнение:
−2(x+1)2+(−5(x+1)((x2−x)+1)+3((x2−x)+1)2)=0
преобразуем:
Вынесем общий множитель за скобки
(x2−3x−1)(3x2−2x+4)=0
Т.к. правая часть ур-ния равна нулю, то решение у ур-ния будет, если хотя бы один из множителей в левой части ур-ния равен нулю.
Получим ур-ния
x2−3x−1=0
3x2−2x+4=0
решаем получившиеся ур-ния:
1.
x2−3x−1=0
Это уравнение вида
a*x^2 + b*x + c = 0
Квадратное уравнение можно решить
с дискриминанта.
Корни квадратного уравнения:
x1=D−−√−b2a
x2=−D−−√−b2a
где D = b^2 - 4*a*c - это дискриминант.
Т.к.
a=1
b=−3
c=−1
, то
D = b^2 - 4 * a * c =
(-3)^2 - 4 * (1) * (-1) = 13
Т.к. D > 0, то уравнение имеет два корня.
x1 = (-b + sqrt(D)) / (2*a)
x2 = (-b - sqrt(D)) / (2*a)
или
x1=32+13−−√2
x2=32−13−−√2
2.
3x2−2x+4=0
Это уравнение вида
a*x^2 + b*x + c = 0
Квадратное уравнение можно решить
с дискриминанта.
Корни квадратного уравнения:
x3=D−−√−b2a
x4=−D−−√−b2a
где D = b^2 - 4*a*c - это дискриминант.
Т.к.
a=3
b=−2
c=4
, то
D = b^2 - 4 * a * c =
(-2)^2 - 4 * (3) * (4) = -44
Т.к. D < 0, то уравнение
не имеет вещественных корней,
но комплексные корни имеются.
x3 = (-b + sqrt(D)) / (2*a)
x4 = (-b - sqrt(D)) / (2*a)
или
x3=13+11−−√i3
x4=13−11−−√i3
Тогда, окончательный ответ:
x1=32+13−−√2
x2=32−13−−√2
x3=13+11−−√i3
x4=13−11−−√i3
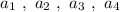 и
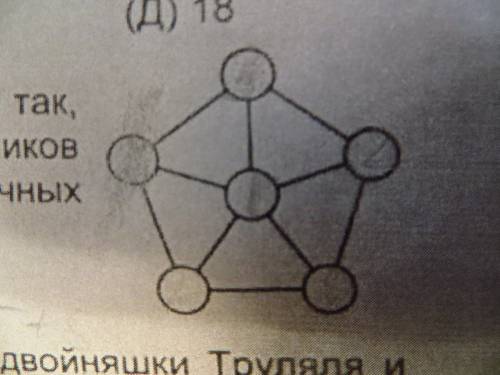
и 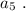 Число, которое стоит в центре обозначим, как
Число, которое стоит в центре обозначим, как 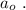

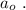

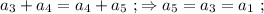
 то:
то: 
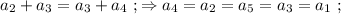
А) через 9 часов после выхода турист был на расстоянии 5 км .
Б) второй привал длился 1 час ( с 7 до 8 )
В) когда до дома осталось пройти 10 км, турист был в пути 7 часов
Г) скорость V=S : t=10 : 2=5 км/час .