Надо бы начертить, но и так будет понятно.
Имеем: Перпендикуляр с середины хорды окружности проходит через центр этой окружности(это из свойств хорды). Середина хорды равна 21:2 = 10,5. Тогда у нас есть прямоугольный треугольник ОВК ( точка К находится в цннтре хорды). ОВ - это радиус = 12 см.
Катет ОК = √r²-10,5² или √33,75.
АК = 10,5 (половина хорды), АС = 9 (это дано) тогда КС = 10,5-9 = 1,5. В прямоугольном треугольнике ОКС имеем ОК = √33,75, КС = 1,5. Тогда квадрат гипотенузы ОС² = (√33,75)² + 1,5² = 33,75 + 2,25 = 36. Значит искомый отрезок ОС = √36 = 6см.
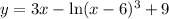
ОДЗ: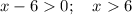 
Найдем производную для заданной функции:
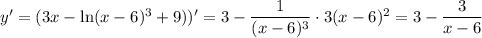
Найдем стационарные (критические) точки. Для этого приравняем производную к нулю:
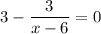
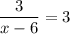
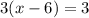
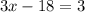
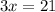
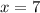
Следовательно, абсцисса 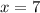— возможно, абсцисса точки экстремума — точка, при переходе через которую производная меняет знак. Если производная меняет знак с "–" на "+", то это точка минимума, если производная меняет знак с "+" на "–", то это точка максимума.
Рассмотрим промежуток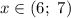 
:
Возьмем, например, абсциссу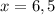 
и подставим ее в производную:
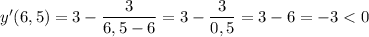
Рассмотрим промежуток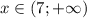 
:
Возьмем, например, абсциссу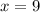 
и подставим ее в производную:
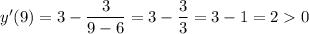
Следовательно, 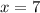— абсцисса точки экстремума, а именно абсцисса точки минимума, так как производная меняет знак с "–" на "+". Тогда значение ординаты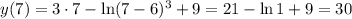 
ответ: точка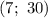 
60 градусов
180-20=60