5. [56] Решите задачу, составив систему уравнений: (решить методом подстановки)
За 3 кг мандаринов и7 кг апельсинов заплатили 4450 тенге. Сколько стоит
1 кг каждого вида фруктов, если 3 кг апельсинов на 50 тенге дешевле, чем 5
кг мандаринов?

👇

Увидеть ответ

Ответ:

podgainiyroma

20.05.2021

Пошаговое объяснение:

/3х + 7у = 4450

\5х - 3у = 50

х = 10 + 0.6у

30 + 1.8у + 7у = 4450

8.8у = 4420

у = 502целых 3/11(тенге) за 1кг. апельсинов

х = 10 + 502 3/11 × 0.6

х = 311целых 4/11(тенге) за 1 кг. мандаринов

4,4(84 оценок)

Открыть все ответы

Ответ:

kantuz

20.05.2021

Начнем строить цепочку.

Удобно начать с числа 16, так как это наибольшее число. Даже если рядом с ним поставить число 15, то их сумма даст 31, а значит все потенциальные квадраты должны быть не больше 31.

Итак, от 16 до 31 есть только один квадрат: 25. Значит, дополняем число 16 до 25 числом 9:

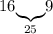
$16 \underset{25}{\underbrace{}} 9$

Число 9 до 25 мы только что дополняли, значит остается только дополнить его до 16 - числом 7:

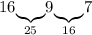
$16 \underset{25}{\underbrace{}} 9\underset{16}{\underbrace{}}7$

Число 7 до 25 дополнить не можем (числа 18 среди карточек нет), значит остается дополнить его до 9 - числом 2:

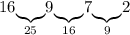
$16 \underset{25}{\underbrace{}} 9\underset{16}{\underbrace{}}7\underset{9}{\underbrace{}}2$

Число 2: до 4 дополнить не можем, так как нужное в этом случае число 2 занято, до 9 дополняли только что, остается дополнить его до 16 - числом 14:

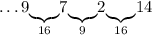
$\ldots9\underset{16}{\underbrace{}}7\underset{9}{\underbrace{}}2\underset{16}{\underbrace{}}14$

Число 14: до 16 дополнить не можем, так как нужное в этом случае число 2 занято, остается дополнить его до 25 - числом 11:

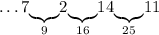
$\ldots7\underset{9}{\underbrace{}}2\underset{16}{\underbrace{}}14\underset{25}{\underbrace{}}11$

Число 11: можем дополнить только до 16 - числом 5:

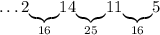
$\ldots2\underset{16}{\underbrace{}}14\underset{25}{\underbrace{}}11\underset{16}{\underbrace{}}5$

Число 5: можем дополнить только до 9 - числом 4:

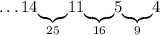
$\ldots14\underset{25}{\underbrace{}}11\underset{16}{\underbrace{}}5\underset{9}{\underbrace{}}4$

Число 4: можем дополнить только до 16 - числом 12:

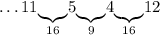
$\ldots11\underset{16}{\underbrace{}}5\underset{9}{\underbrace{}}4\underset{16}{\underbrace{}}12$

Число 12: можем дополнить только до 25 - числом 13:

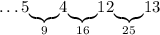
$\ldots5\underset{9}{\underbrace{}}4\underset{16}{\underbrace{}}12\underset{25}{\underbrace{}}13$

Число 13: можем дополнить только до 16 - числом 3:

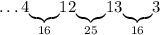
$\ldots4\underset{16}{\underbrace{}}12\underset{25}{\underbrace{}}13\underset{16}{\underbrace{}}3$

Число 3. Только на этом шаге возникает несколько вариантов. Мы можем дополнить его до 4 или до 9. Пробуем дополнить до 4 - числом 1:

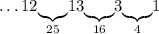
$\ldots12\underset{25}{\underbrace{}}13\underset{16}{\underbrace{}}3\underset{4}{\underbrace{}}1$

Число 1. Опять же, мы можем дополнить его до 9 или до 16. Пробуем дополнить до 9 - числом 8:

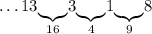
$\ldots13\underset{16}{\underbrace{}}3\underset{4}{\underbrace{}}1\underset{9}{\underbrace{}}8$

Число 8. До 9 его мы дополняли только что, до 16 дополнить его не можем (отсутствует еще одна восьмерка), до 25 также дополнить не можем (карточки 17 у нас нет). Тупик.

Значит, нужно вернуться назад и попробовать дополнить число 1 до 16 - числом 15:

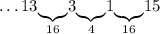
$\ldots13\underset{16}{\underbrace{}}3\underset{4}{\underbrace{}}1\underset{16}{\underbrace{}}15$

Число 15: можем дополнить только до 25 - числом 10:

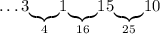
$\ldots3\underset{4}{\underbrace{}}1\underset{16}{\underbrace{}}15\underset{25}{\underbrace{}}10$

Число 10: можем дополнить только до 16 - числом 6:

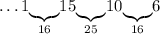
$\ldots1\underset{16}{\underbrace{}}15\underset{25}{\underbrace{}}10\underset{16}{\underbrace{}}6$

Число 6. Для дополнения его до 9 нам нужна карточка 3, а она занята, до 16 мы его дополняли только что. Вновь тупик.

В этом случае, снова возвращаемся назад и дополняем число 13 до 9 - числом 6:

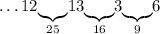
$\ldots12\underset{25}{\underbrace{}}13\underset{16}{\underbrace{}}3\underset{9}{\underbrace{}}6$

Число 6: можем дополнить только до 16 - числом 10:

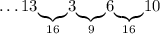
$\ldots13\underset{16}{\underbrace{}}3\underset{9}{\underbrace{}}6\underset{16}{\underbrace{}}10$

Число 10: можем дополнить только до 25 - числом 15:

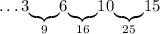
$\ldots3\underset{9}{\underbrace{}}6\underset{16}{\underbrace{}}10\underset{25}{\underbrace{}}15$

Число 15: можем дополнить только до 16 - числом 1:

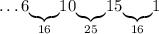
$\ldots6\underset{16}{\underbrace{}}10\underset{25}{\underbrace{}}15\underset{16}{\underbrace{}}1$

Число 1: дополняем единственным оставшимся числом 8 - до 9:

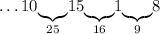
$\ldots10\underset{25}{\underbrace{}}15\underset{16}{\underbrace{}}1\underset{9}{\underbrace{}}8$

Таким образом, ряд чисел составить получилось:

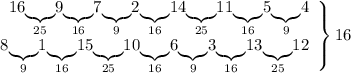
$\left\begin{array}{r}16 \underset{25}{\underbrace{}} 9\underset{16}{\underbrace{}}7\underset{9}{\underbrace{}}2\underset{16}{\underbrace{}}14\underset{25}{\underbrace{}}11\underset{16}{\underbrace{}}5\underset{9}{\underbrace{}}4 \\ 8\underset{9}{\underbrace{}}1\underset{16}{\underbrace{}}15\underset{25}{\underbrace{}}10\underset{16}{\underbrace{}}6\underset{9}{\underbrace{}}3\underset{16}{\underbrace{}}13\underset{25}{\underbrace{}}12\end{array}\right\}16$

Однако, этот ряд не закольцовывается, так как сумма первого и последнего элемента равна 24 и не является квадратом.

Таким образом, выложить в ряд у Васи получится, а выложить по кругу у Пети не получится.

ответ: у Пети - нет, у Васи - да

4,7(73 оценок)

Ответ:

варя373

20.05.2021

Поиск...

Избавься от ограничений

ПОПРОБУЙ ЗНАНИЯ ПЛЮС СЕГОДНЯ

цветок93

14.04.2018

Геометрия

5 - 9 классы

ответ дан • проверенный экспертом

что можно сказать о взаимном расположении прямой и окружности, если диаметр окружности равен 10,3 см, а расстояниеот центра окружности до прямой равно 4,15см; 2 дм; 103мм; 5,15 см; 1 дм 3 см сделать к сегодняшнему дню очненььь

СМОТРЕТЬ ОТВЕТ

Войди чтобы добавить комментарий

ответ, проверенный экспертом

4,5/5

175

potapov19461

светило науки

4.6 тыс. ответов

12.2 млн пользователей, получивших

Нужно сравнить радиус и расстояние от центра окружности до прямой.

Радиус равен 10,3см/2 = 5,15 см.

5,15см >4,15см⇒ окружность и прямая пересекаются.