Треугольник ABC - равнобедренный (AB = BC), AC = 30 см, AD и BE - высоты треугольника. На какую длину точка D делит боковую сторону BC, если AD = 24 см и BE = 20 см?

Треугольник ABC - равнобедренный (AB = BC), AC = 30 см, AD и BE - высоты треугольника. На какую длин

👇

Увидеть ответ

Ответ:

winx237

05.11.2022

вд=7см; дс=18см

Пошаговое объяснение:

треугольник равнобедренный значит высота ве проведенная к основанию является медианой и биссектрисой

ае=ес=30:2=15см

Рассмотрим треугольник вес- прчмоугольный

По теореме Пифагора а^2+в^2=с^2

20^2+15^=с^2

400+225=с^2

с^2=625

с=25

вс=25см

ав=вс=25см

Рассмотрим треугольник вад- прямоугольный

а^2+в^2=с^2

24^2+в^2=25^2

в^2=625-576

в^2=49

в=7

вд=7см

вс=вд+дс

25см=7см+дс

дс=25см-7см=18см

ответ:вд=7см;дс=18см

4,4(65 оценок)

Открыть все ответы

Ответ:

kanat9809

05.11.2022

7/8 * 64 = 7 * 8 = 56,

5/8 * 4/25 = 1/10,

5/8 * 9 1/7 = 5/8 * 64/7 = 40/7 = 5 5/7,

0,15 * 40 = 15/100 * 40 = 3 * 2 = 6,

0,65 * 3/13 = 65/100 * 3/13 = 15/100 = 3/20,

32 * 5/8 = 4 * 5 = 20 кустов гортензии,

7 1/5 * 5/9 = 36/5 * 5/9 = 4 см - 2 сторона,

Р = 2 * (7 1/5 + 4) = 2 * 11 1/5 = 2 * 56/5 = 112/5 = 22 2/5 см - периметр,

S = 7 1/5 * 4 = 36/5 * 4 = 144/5 = 28 4/5 см² - площадь,

100% - 8% = 92% - процент содержания железа,

360 * 0,92 = 360 * 92/100 = 1656/5 = 331 1/5 кг - железа,

360 * 0,08 = 360 * 8/100 = 28 4/5 кг - меди,

360 - 28 4/5 = 359 5/5 - 28 4/5 = 331 1/5 кг - железа,

(5 2/5 - 1 5/6 + 3 4/15) * 2 2/5 - 3 2/3 = 12 11/15,

1) 5 2/5 - 1 5/6 + 3 4/15 = 5 12/30 - 1 25/30 + 3 8/30 =

= 4 42/30 - 1 25/30 + 3 8/30 = 6 25/30 = 6 5/6,

2) 6 5/6 * 2 2/5 = 41/6 * 12/5 = 82/5 = 16 2/5,

3) 16 2/5 - 3 2/3 = 16 6/15 - 3 10/15 = 15 21/15 - 3 10/15 = 12 11/15

4,4(74 оценок)

Ответ:

Anway2017

05.11.2022

1. Найдите значение производной функции в точке x₀:

a) y=(3·x-2)⁷, x₀=3

y'=((3·x-2)⁷)'=7·(3·x-2)⁶·(3·x-2)'=7·(3·x-2)⁶·3=21·(3·x-2)⁶

y'(3)=21·(3·3-2)⁶=21·7⁶=21·117649=2470629

б) y=(4-5·x)⁷, x₀=1

y'=((4-5·x)⁷)'=7·(4-5·x)⁶·(4-5·x)'=7·(4-5·x)⁶·(-5)= -35·(4-5·x)⁶

y'(1)= -35·(4-5·1)⁶= -35·(-1)⁶= -35·1= -35

в) y=(2·x+3)⁵, x₀=2

y'=((2·x+3)⁵)'=5·(2·x+3)⁴·(2·x+3)'=5·(2·x+3)⁴·2=10·(2·x+3)⁴

y'(2)=10·(2·2+3)⁴=10·7⁴=10·2401=24010

г) y=(5-3·x)⁷, x₀=1

y'=((5-3·x)⁷)'=7·(5-3·x)⁶·(5-3·x)'=7·(5-3·x)⁶·(-3)= -21·(5-3·x)⁶

y'(1)= -21·(5-3·1)⁶= -21·2⁶= -21·64= -1344

2. Вычислить скорость изменения функции в точке x₀ (скорость изменения равносильно производная первого порядка):

a) y=(2x+1)⁵, x₀= -1

y'=((2·x+1)⁵)'=5·(2·x+1)⁴·(2·x+1)'=5·(2·x+1)⁴·2=10·(2·x+1)⁴

y'(-1)=10·(2·(-1)+1)⁴=10·(-1)⁴=10·1=10

б) 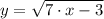$\displaystyle y=\sqrt{7 \cdot x-3}$ , x₀= 1

$\displaystyle y'=(\sqrt{7 \cdot x-3})' =((7 \cdot x-3)^{\frac{1}{2} })'=\dfrac{1}{2} \cdot (7 \cdot x-3)^{\frac{1}{2}-1} \cdot (7 \cdot x-3)'=\\\\=\dfrac{1}{2} \cdot (7 \cdot x-3)^{-\frac{1}{2}} \cdot 7=\dfrac{7}{2} \cdot (7 \cdot x-3)^{-\frac{1}{2}}$

$\displaystyle y'(1)=\dfrac{7}{2} \cdot (7 \cdot 1-3)^{-\frac{1}{2}}=\dfrac{7}{2} \cdot 4^{-\frac{1}{2}}=\dfrac{7}{2} \cdot 2^{-1}= \dfrac{7}{2} \cdot\frac{1}{2}=\dfrac{7}{4}=1\dfrac{3}{4}$

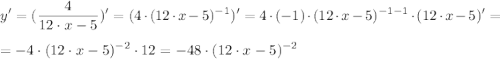
в) $\displaystyle y=\frac{4}{12 \cdot x-5}$ , x₀= 2 $\displaystyle$ $\displaystyle y'=(\frac{4}{12 \cdot x-5})'=(4 \cdot (12 \cdot x-5)^{-1})'=4 \cdot (-1) \cdot (12 \cdot x-5)^{-1-1} \cdot (12 \cdot x-5)'=\\\\=-4 \cdot (12 \cdot x-5)^{-2} \cdot 12=-48 \cdot (12 \cdot x-5)^{-2}$

$\displaystyle y'(2)=-48 \cdot (12 \cdot 2-5)^{-2}= \frac{-48 }{19^{2}}=-\frac{48 }{361}}$

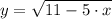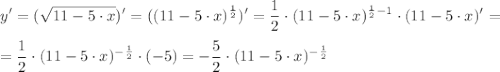
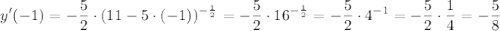
г) $\displaystyle y=\sqrt{11-5 \cdot x}$ , x₀= -1 $\displaystyle y'=(\sqrt{11-5 \cdot x})' =((11-5 \cdot x)^{\frac{1}{2} })'=\dfrac{1}{2} \cdot (11-5 \cdot x)^{\frac{1}{2}-1} \cdot (11-5 \cdot x)'=\\\\=\dfrac{1}{2} \cdot (11-5 \cdot x)^{-\frac{1}{2}} \cdot (-5)=-\dfrac{5}{2} \cdot (11-5 \cdot x)^{-\frac{1}{2}}$ $\displaystyle y'(-1)=-\dfrac{5}{2} \cdot (11-5 \cdot (-1))^{-\frac{1}{2}}=-\dfrac{5}{2} \cdot 16^{-\frac{1}{2}}=-\dfrac{5}{2} \cdot 4^{-1}= -\dfrac{5}{2} \cdot \frac{1}{4}=-\dfrac{5}{8}$

3. Найдите производные функций:

a) y=(x-1)·(x²+x+1) = x³-1

=1·(x²+x+1)+(x-1)·(2·x+1)= x²+x+1+2·x²+x-2·x-1 =3·x²

б) $\displaystyle y=\frac{x^{9}-3}{x^{3}}$

$\displaystyle y'=(\dfrac{x^{9}-3}{x^{3}})'=\dfrac{(x^{9}-3)' \cdot x^{3}-(x^{3})' \cdot (x^{9}-3)}{(x^{3})^{2}}=\\\\=\dfrac{(9 \cdot x^{8}-0) \cdot x^{3}-(3 \cdot x^{2}) \cdot (x^{9}-3)}{x^{6}}=\dfrac{9 \cdot x^{8}\cdot x^{3}-3 \cdot x^{2} \cdot (x^{9}-3)}{x^{6}}=\\\\=\dfrac{9 \cdot x^{11}-3 \cdot x^{11} +9\cdot x^{2}}{x^{6}}=\dfrac{6 \cdot x^{11}+9\cdot x^{2}}{x^{6}}=\dfrac{6 \cdot x^{9}+9}{x^{4}}$

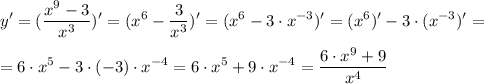
$\displaystyle y'=(\dfrac{x^{9}-3}{x^{3}})'=(x^{6}-\dfrac{3}{x^{3}})'=(x^{6}-3 \cdot x^{-3})'=(x^{6})'-3 \cdot (x^{-3})'=\\\\= 6 \cdot x^{5}-3 \cdot (-3) \cdot x^{-4}=6 \cdot x^{5}+9\cdot x^{-4}=\dfrac{6 \cdot x^{9}+9}{x^{4}}$