Теорема Безу
Остаток от деления многочлена f(x) на двучлен (x - a) равен f(a)
Доказательство
f(x) = (x - a)·g(x) + r, где g(x) - частное, имеет степень на 1 меньше, чем f(x), а r - число (многочлен степени 0)
Тогда, подставляя x = a получаем:
f(a) = (a - a)·g(a) + r, то есть получаем f(a) = r, или r = f(a) - что и требовалось.
Теорема 2
x = a - корень f(x) ⇔ f(x) делится на (x - a)
Доказательство
из теоремы Безу получаем, что если f(a) = 0 (то есть a - корень f(x)) ⇒ f(x) = (x - a)·g(x) + 0 ⇒ f(x) при делении на (x - a) дает g(x) при 0-м остатке, а значит делится (x - a)
Обратно: раз f(x) делится на (x - a), значит остаток равен 0, а он по теореме Безу равен f(a), то есть a - корень f(x)
Пусть в первом куске, массой 12кг, содержание свинца в процентах равно "а", а во втором куске, массой 36кг, равно "b".
Обозначим массу отрезаемых кусков за "x".
Тогда после отрезания "x" килограммов от первого куска, там останется (12-x)кг, т.к. содержание свинца в этом остатке "а", то свинца в остатке будет (12-х)*а.
Отрезок от первого куска будет содержать x*a свинца.
После отрезания "x" килограммов от второго куска, там останется (36-x)кг, т.к. содержание свинца в этом остатке "b", то свинца в остатке будет (12-х)*b.
Отрезок от второго куска будет содержать x*b свинца.
Т.к. отрезки поменяли местами и сплавили, то получившиеся куски сплавов будут иметь такую же массу, как и в начале (отрезали и потом прибавляли куски одинаковой массы), т.е. 12 и 36 кг.
Содержание свинца в новом первом куске будет (12-х)*а+x*b
Содержание свинца в новом втором куске будет (36-х)*b+x*a
Процентное содержание свинца в новом первом куске будет 
Процентное содержание свинца в новом втором куске будет 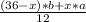
Т.к. в итоге процентное содержание стало равным, то можно приравнять последние два выражения:

Раскроем скобки в числителях и умножим обе части на 36:

Соберем слагаемые с "х" справа, а остальное - слева:
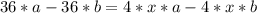
Вынесем общие множители: справа - 4*х, а слева - 36

Сократим на (а-b)

Отсюда x=9
ответ: 9 кг
Відповідь:
60; 120
Покрокове пояснення: