Периметр прямоугольника равен :
(4+ 8) * 2 = 24 см
Сторона квадрата равна : 24/ 4 = 6 см
Площадь квадрата равна : 6*6 = 36см2
(в приложении рисунок)
Вот смотри. Мы начертили произвольный четырехугольник ABCD и отметили все точки, какие было нужно, а теперь будем рассматривать треугольник ABC и треугольник IBJ. Нам нужно доказать, что IJ=1/2AC, иначе говоря, оказать, что AC=2IJ. Что мы имеем? AI=IB, так как I - это середина AB; BJ=JC, так как J - это середина BC. Тогда AB=2BI, а BC=2BJ. Так же ΔABC и ΔIBJ имеют общий угол B, то есть ∠АВС=∠IBJ. И теперь мы видим что ΔABC и ΔIBJ подобны по второму признаку подобия треугольников, по двум сторонам и углу между ними (
и ∠АВС=∠IBJ). Подобные треугольники - это треугольники, углы у которых соответственно равны, а стороны соответственно пропорциональны. В таком случае, все стороны пропорциональны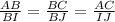 
. Теперь найдем их пропорциональное соотношение:
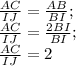
или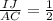 
.
P.S. Вот и всё, надеюсь, понятно.
См. "Пошаговое объяснение".
Пошаговое объяснение:
1) Так как две соседние стороны образуют с диагональю равные углы, то это значит, что все 4 угла между сторонами прямоугольника равны:
90° : 2 = 45° .
2) Действительно, противоположные стороны прямоугольника параллельны, а его диагональ для этих параллельных является секущей. Образуется две пары накрест лежащих углов, которые равны между собой.
3) Следовательно, диагональ такого прямоугольника разбивает его на 2 равнобедренных треугольника, в котором основанием является диагональ, а боковыми сторонами - стороны одинаковой длины.
Таким образом, данный прямоугольник является квадратом, что и требовалось доказать.
36
Пошаговое объяснение:
P(прямоугольника)=2(a+b)=2(8+4)=24
P(квадрата)=4a=24
a=24/4
a=6
S(квадрата)=a*a=6*6=36