(х-3,5)×2.3=24,15
х-3.5=24,15/2,3
х-3,5=10,5
х=10,5+3,5
х=14
Пошаговое объяснение:
(14-3,5)×2,3=24,15
Итак у нас тут было неизвестно уменьшаемое то есть X и вот нашли ответ.
уравнение обычно решается логично нужно тут логика.Давайте подумаем если 24,15 это ответ то 24,15 мы нашли это что мы умножили ответ скобки на 2,3... А чтобы решить нужно наоборот делить. получили ответ теперь к этому ответу нужно прибавить 3,5 и проверить Правильно ли.
В уравнении все наоборот + становиться -,- становиться +, × становиться ÷
но иногда нет. есть разные случаи..
ответ: нет
Заметим, что на стороне разрезанного треугольника ABC должна быть хотя бы одна вершина меньших треугольников, отличная от A, B и C.
Пойдем от противного. Допустим, что есть сторона, не содержащая таких вершин. Но тогда получается, что она принадлежит какому-то из меньших треугольников. Т.к. меньший треугольник тоже правильный, получим, что он совпадает с ABC. Противоречие.
А значит на стороне треугольника ABC есть хотя бы одна такая точка.
Без нарушения общности допустим, что это точка E∈AC.
Далее заметим, что, т.к. у правильного треугольника все углы равны 60°, а развернутый угол CEA = 180°=3*60°, то эта вершина принадлежит трем меньшим треугольникам.
Отложим луч EE', E'∈AB, ∠AEE'=60°. Тогда получим, что EE'B=60°+60°=120°(как внешний для треугольника AEE')=EE'C.
Аналогичными рассуждениями строим отрезки ED и E'D', ∠EE'D'=∠E'ED=60°, D∈BC, D'∈BC. Точку пересечения ED и E'D', если она есть, обозначим через H.
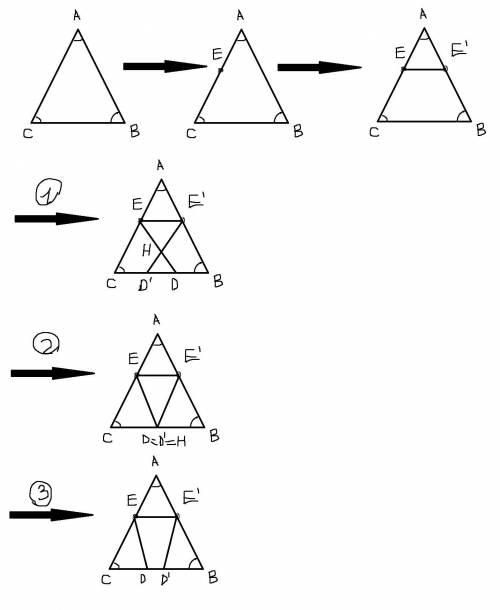
Здесь возможны 3 случая (см. приложение к ответу):
Получили 5 частей, из которых 2 - не треугольники. А значит в этом случае разрезать нельзя.Получили 4 правильных треугольника. Значит один из них нужно разрезать на 2 правильных. Проведя рассуждения, аналогичные рассуждениям выше про треугольник ABC, для любого из этих треугольников, понимаем, что это невозможно. А значит в этом случае разрезать нельзя.Получили 3 правильных треугольника и одну трапецию. Очевидно, что ее надо разрезать на 2 правильных треугольника. Т.к. EE'D'=60°, то очевидно, что для разреза нам необходимо построить отрезок XX', X'∈E'D', X∈EE' (X∉ED, потому что в этом случае получаем 2 четырехугольника, и уже после этого шага всего 5 фигур, а значит разрезать их на более мелкие части не получится), ∠E'X'X=∠X'XE'=60°. Однако заметим, что ED||XX' (∠E'ED=60°, ∠X'XE'=60°, EE' - секущая), а значит после разреза получим треугольник и фигуру, которая не треугольник (есть 2 параллельные стороны), и в сумме уже 5 фигур, а значит фигуру разрезать на более мелкие уже нельзя. А значит в этом случае разрезать нельзя.А значит удовлетворяющие условию задачи разрезания выполнить нельзя.
14
Пошаговое объяснение:
(24,15 :2,3)+3.5=14