Решение
Пусть B — вершина тупого угла ромба ABCD, BK — его высота, опущенная на сторону AD. Поскольку AB = = 2, а BK = 1, то < BКC = 30o.
Поэтому < ABC = 180o - 30o = 150o.
ответ: 150°
Відповідь:
Покрокове пояснення:
а1 - проекція катета а на гіпотенузу
b1 - проекція катета b на гіпотенузу
a^2 = c*a1; b^2 c*b
а) c = 6 + 24 = 30 см
a^2 = 30*6 = 180
a =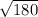 
= 6
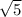см
b^2 = 30*24 = 720
b =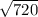 
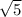= 12 см
б) c = 12 + 16 = 28
a^2 = 28*12 = 336
a =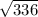 
= 16
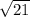см
b^2 = 28*16 = 448
b =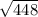 
= 16
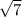см
в) c = 8 + 10 = 18 см
a^2 = 18*8 = 144
a =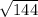 
= 12 см
b^2 = 18*10 = 180
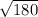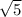b = = 6 см
г) c = 3 + 23 = 26
a^2 = 26*3 = 78
a =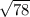 
см
b^2 = 26*23 = 598
b =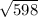 
см
Пошаговое объяснение:
Дано: ABCD - ромб, Периметр ромба =8 cм, СМ=1 см, Найти: Угол A (тупой) Решение: т.к. AB=BC=AD=CD следовательно, ВС=1/4 периметра АВСД=2 см Рассмотрим треугольник МВС: СМ=1 см, ВС=2 см следовательно, угол В=30 градусов (т.к. напротив угла в 30 градусов лежит 1/2 гипотенузы).