Найдем сначала общее решение соответствующего однородного уравнения:
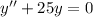
Пусть  , получим характеристическое уравнение:
, получим характеристическое уравнение:
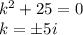
Характеристическое уравнение имеет два комплексных корня Два линейно независимые решения это 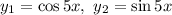
Общее решение однородного дифференциального уравнения:
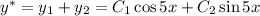
Рассмотрим правую часть дифференциального уравнения:
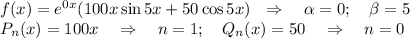
Число 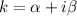 принимает значение
принимает значение 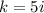 , это число является корнем характеристическое уравнение
, это число является корнем характеристическое уравнение 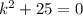 . Кратность k=1
. Кратность k=1
Частное решение будем искать в виде:
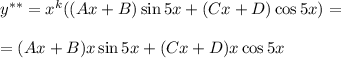
Вычислим для нее производную второго порядка
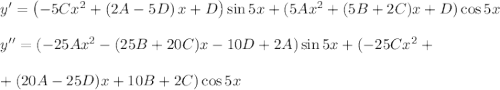
Подставив в исходное дифференциальное уравнение, получим:
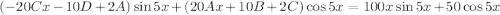
Приравниваем коэффициенты при xcos5x, xsin5x, sin5x, cos5x, получим систему уравнений:
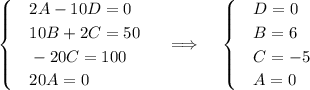
Частное решение: 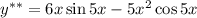
Общее решение линейного неоднородного дифференциального уравнения:
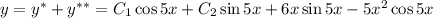
что бы сумма его цифр делилось на 9.
Значит сумма цифр трехзначного числа равна 18.
Так как максимальное 27 может быть у 999, но его частное 111 не подходит.
А если сумма цифр равна 9 то вряд ли сумма цифр его частного 9-9=0 (нуль).
Значит сумма цифр частного равна 18-9=9.
Есть следующие варианты
18*9=162 (Сумма цифр 1+6+2=9) - Не подходит
27*9=243 (Сумма цифр 9) - Не подходит
36*9=324 (Сумма цифр 9) - Не подходит
45*9=405 (Сумма цифр 9) - Не подходит
54*9=486 (Сумма цифр 18) - Подходит
63*9=567 (Сумма цифр 18) - Подходит
72*9=648 (Сумма цифр 18) - Подходит
81*9=729 (Сумма цифр 18) - Подходит
90*9=810 (Сумма цифр 9) -Не подходит
108*9=972 (Сумма цифр 18) - Подходит
117=1053 перебор - Не подходит
ответ: 486,567,648,729, 972.