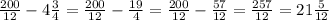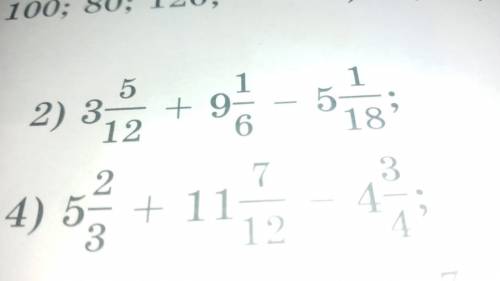
Любое геометрическое тело состоит из оболочки, т. е. внешней поверхности, и какого-либо материала, его наполняющего . Каждое геометрическое тело имеет свою форму, которая различается по составу, структуре и размерам.
Состав формы геометрического тела — перечень отсеков поверхностей, составляющих его (табл. 4). Так, форма прямоугольного параллелепипеда состоит из шести отсеков, поверхностей (граней): две из них являются основаниями параллелепипеда, а остальные четыре отсека образуют замкнутую выпуклую ломаную поверхность, называемую боковой поверхностью.
2)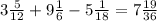
4)
Пошаговое объяснение:
2)
1)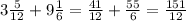
2)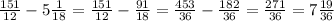
4)
1)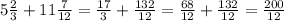
2)