а) При значении а = -6 уравнение имеет корень равный 2.
При значении а = 16 уравнение имеет корень равный -3/4.
При значении а = 60 уравнение имеет корень равный -0,2.
b) При значении а = 0 уравнение не имеет корней.
c) При а > 0 уравнение будет иметь отрицательный корень.
Пошаговое объяснение:
Требуется найти, при каких значениях а уравнение
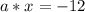 :
:
а)
1. Имеет корень, равный 2.
Подставим вместо х его значение 2 и решим уравнение относительно а:
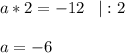
⇒ При значении а = -6 уравнение имеет корень равный 2.
2. Имеет корень, равный 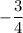 .
.
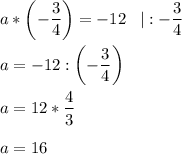
⇒ При значении а = 16 уравнение имеет корень равный 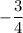 .
.
3. Имеет корень, равный -0,2.
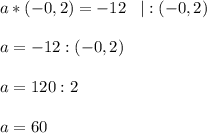
⇒ При значении а = 60 уравнение имеет корень равный -0,2.
b) Не имеет корней.
Уравнение не имеет решения, если при любом значении х, мы не получим верного равенства.Это возможно только тогда, когда а = 0.
Проверим:
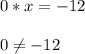
⇒ При значении а = 0 уравнение не имеет корней.
с) Имеет отрицательный корень.
Правая часть у нас отрицательная.
При нахождении корня, мы делим правую часть на а. Чтобы корень был отрицательным, то а должно быть положительным.
При делении чисел с разными знаками, частное - отрицательно.⇒ а > 0
⇒ При а > 0 уравнение имеет отрицательный корень.
1 дм > 9 см, 1 см = 10 мм, 1 м > 90 см, 2 см 8 мм > 10 мм, 1 дм 7см > 10 см, 4 м 50 см > 100 см.
Пошаговое объяснение:
1 дм > 9 см: 1 дм = 10 см, 10 см > 9 см. Значит, 1 дм больше.
1 м > 90 см: 1 м = 100 см, 100 см > 90 см. Значит, 1 м больше.
2 см 8 мм > 10 мм: 2 см 8 мм = 28 мм, 28 мм > 10 мм. Значит, 2 см 8 мм больше.
1 дм 7см > 10 см: 1 дм 7 см = 17 см, 17 см > 10 см. Значит, 1 дм 7 см больше.
4 м 50 см > 100 см: 4 м 50 см = 450 см, 450 см > 100 см. Значит, 4 м 50 см больше.
Дана функция f(x) = 8x^3+9x^2+3x+2.
Её производная равна y' = 24x^2 + 18x + 3 = 3(8x^2 + 6x + 1).
Приравняем её нулю (достаточно выражение в скобках):
8x^2 + 6x + 1 = 0, Д = 36 - 4*8*1 = 4,
х1 = (-6 - 2)/(2*8) = -1/2,
х2 = (-6 + 2)/(2*8) = -1/4.
Найдены 2 критические точки.
Определяем их свойства по знаку производной левее и правее этих точек.
x = -0,6 -0,5 -0,4 -0,25 -0,2
y' = 0,84 0 -0,36 0 0,36.
Как видим, максимум в точке х = -0,5, а минимум в точке х = -0,25.
Значения функции в критических точках:
y(min) = 27/16 при x = -1/4,
y(max) = 7/4 при x = -1/2.