
 заявленный и в приведённом условии. Далее порассуждаем практически:
заявленный и в приведённом условии. Далее порассуждаем практически: ;
; ;
;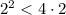 ;
; ;
;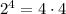 ;
;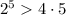 ;
; производная
производная 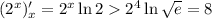 больше производной
больше производной 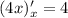 , т.е. дальше левая часть уравнения, растёт быстрее, чем правая, а значит, других корней при
, т.е. дальше левая часть уравнения, растёт быстрее, чем правая, а значит, других корней при  быть не может.
быть не может.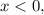 левая часть уравнения положительна, а правая отрицательна, так что других корней при
левая часть уравнения положительна, а правая отрицательна, так что других корней при  быть не может.
быть не может.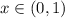 , так как при сравнении двух непрерывных функций на этом интервале меняется знак.
, так как при сравнении двух непрерывных функций на этом интервале меняется знак.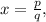 где
где 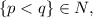 то:
то: ![2^x = 2^\frac{p}{q} = (\sqrt[q]2)^p < 2 .](/tpl/images/0486/4079/dd2eb.png) Это число, очевидно иррационально, что легко доказать от обратного методом Евклида. Однако справа должно быть рациональное число
Это число, очевидно иррационально, что легко доказать от обратного методом Евклида. Однако справа должно быть рациональное число 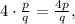 а значит, мы пришли к противоречию. Таким образом, второе решение иррационально.
а значит, мы пришли к противоречию. Таким образом, второе решение иррационально.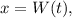 по определению дающая решение, т.е. являющаяся обратной, к функции
по определению дающая решение, т.е. являющаяся обратной, к функции  Функция вводится аналогично, скажем, функции
Функция вводится аналогично, скажем, функции 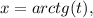 являющейся решением уравнения
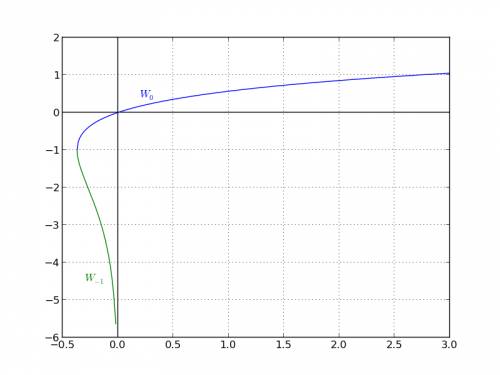
являющейся решением уравнения  но в отличие от арктангенса, функция Ламберта используется намного реже в прикладных задачах (в основном в задачах теплопроводности), и поэтому – менее широко известна. Функция вводится на расширенной комплексной плоскости, т.е. алгебраически, а не арифметически, а значит по определению, может быть многозначной, и является таковой при отрицательных значениях аргумента
но в отличие от арктангенса, функция Ламберта используется намного реже в прикладных задачах (в основном в задачах теплопроводности), и поэтому – менее широко известна. Функция вводится на расширенной комплексной плоскости, т.е. алгебраически, а не арифметически, а значит по определению, может быть многозначной, и является таковой при отрицательных значениях аргумента 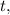 хотя нам достаточно будет знать лишь её действительные значения, которых при отрицательных аргументах всегда два. Вид действительных ветвей функции Ламберта представлен на приложенном изображении.
хотя нам достаточно будет знать лишь её действительные значения, которых при отрицательных аргументах всегда два. Вид действительных ветвей функции Ламберта представлен на приложенном изображении.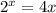 ;
;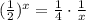 ;
; ;
;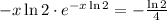 ;
;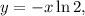 тогда:
тогда: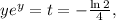 отсюда через функцию Ламберта:
отсюда через функцию Ламберта:
 ;
;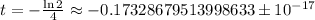 равна:
равна: ;
; искомое значение и вычисляя
искомое значение и вычисляя 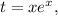 добиваясь его равенства
добиваясь его равенства 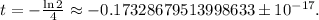
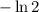 как раз и даст значение
как раз и даст значение  , что можно легко проверить подстановкой.
, что можно легко проверить подстановкой.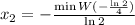 ;
;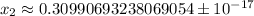 ;
;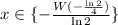 ;
; ;
;
а)2x(x-3)-3x(x+5)=2x^2-6x-3x^2-15x=x^2-21x=x(x-21)
б)(а+7)(а-1)+(а-3)^2=a^2-7+6a+a^2+9-6a=2a^2+2=2(a^2+1)
№2 Разложите на множители а)с^2-16c =c(c-16)
b)3a^2-6ab+3b^2 =3(a-b)^2
№3 Упростите выр-е
(3a-a^2)^2-a^2(a-2)(a+2)+2a(7+3a^2)=9a^2+a^4-6a^3-a^4+4a^2+14a+6a^3=13a^2+14a
№4 разложите на множители а)81a^4-1=(9a^2+1)(9a^2-1)=(9a^2+1)(3a+1)(3a-1)
b)y^2-x^2-6x-9=y^2-(x+3)^2=(y-x-3)(y+x+3)