
1. НОД(А,В) = 2²⁸*3²⁹
НОК(А,В) = 2⁶⁵*3⁷⁴*5²⁸
2. а) 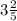 ; б)
; б) 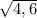
Пошаговое объяснение:
Задание 1.
А= 2³⁷*3¹⁵*12¹⁴ = 2³⁷*3¹⁵*(2²*3)¹⁴ = 2³⁷*3¹⁵*2²⁸*3¹⁴ = 2³⁷⁺²⁸ * 3¹⁵⁺¹⁴ = 2⁶⁵*3²⁹
В = 3⁷⁴ *10²⁸ = 3⁷⁴ *(2*5)²⁸ = 3⁷⁴*2²⁸*5²⁸
НОД(А,В) = 2²⁸*3²⁹
НОК(А,В) = 2⁶⁵*3⁷⁴*5²⁸
Задание 2.
a) x∈[√11; √13] и x∈Q (Q- множество рациональных чисел)
x=?
√11 ≈ 3,32 √13 ≈ 3,66
3,32 < x < 3,66
Например, x= 3,4 = 3 4/10 = 3 2/5 (∈Q)
x= 3,5 = 3 5/10 = 3 1/2 (∈Q)
x= 3,6 = 3 6/10 = 3 3/5 (∈Q)
(приведено сразу 3 примера такого рационального числа, на самом деле, их бесконечное множество).
б) x∈[2,1; 2,2], x∈I (I - множество иррациональных чисел)
2,1 = √(2,1)² = √4,41
2,2 = √(2,2)² = √4,84
√4,41 < x < √4,84
Например, х=√4,6 или х=√4,71 или х=√4,782 или х=√4,815
(приведено сразу 4 примера такого иррационального числа, на самом деле, их бесконечное множество).