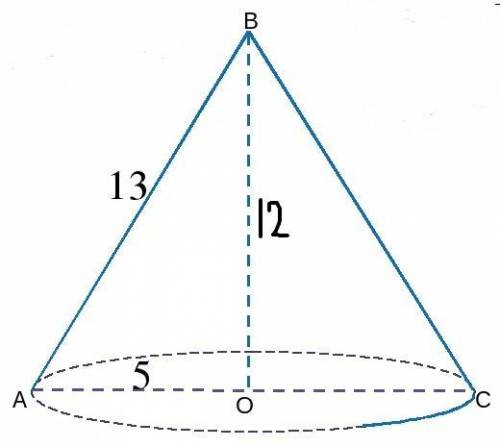
Высота конуса 12 см,диаметр основания 10 см. найдите площадь боковой поверхности конуса.
Площадь боковой поверхности конуса находим по формуле:
S бок. = ПRl, где R - радиус основания конуса, L - длина его образующей.
Найдем образующую конуса АВ по теореме Пифагора:
АВ² = ВО² + АО²
АО - радиус основания. Радиус равен половине диаметра. Т.е АО = 5 см.
Тогда:
АВ² = 5² + 12²
АВ² = 25 + 144
АВ² = 169
АВ = 13
Значит АВ = 13 см.
Поставим имеющиеся значения и найдем искомую величину:
S(бок) = п * 5 * 13 = 65п (см²)
ответ: 65п (см²)
P=21см
S=24.5см^2
Пошаговое объяснение:
1)находим длинну:7*0.5=3.5(см)
2)P=2*(a+b)=2*(7+3.5)=2*10.5=21(см)
3)S=a*b=7*3.5=24.5см^2
Объяснение:
как мы знаем длинна больше чем ширина,но есть и такой тип прямоугольника:
||
| |
| |
| |
| |
||
что и видим, что длинна меньше чем ширина
символ "^"ето степень