В действительных числах 2 решения: х = -3 или х = 1
В комплексных 4 решения: х = -3 или х = 1 или 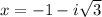 или
или 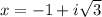
Пошаговое объяснение:
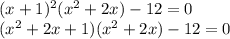
Пусть t = x² + 2x, тогда уравнение имеет вид
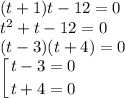
Решим каждое из уравнений по отдельности.
Первое уравнение
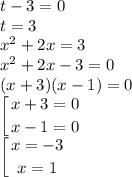
Нашли 2 корня х = -3 или х = 1
Второе уравнение
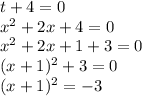
В действительных числах решений нет, так как квадрат отрицателен.
Но давайте все же посчитаем (так как уровень студенческий)
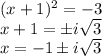
Получаем в действительных числах 2 решения: х = -3 или х = 1
и в комплексных 4 решения: х = -3 или х = 1 или 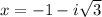 или
или 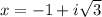
1) В любой треугольник можно вписать окружность.
5) Любые два равносторонних треугольника подобны.
По первому признаку подобия треугольников - любые равносторонние треугольники будут подобны, т.к. 2 угла одного треугольника равны 2-ум углам другого (по 60°)
НЕ ВЕРНЫЕ УТВЕРЖДЕНИЯ:
2) Любые два прямоугольных треугольника подобны.
НЕТ, необходимо, чтобы 2 угла были равны, по первому признаку подобия треугольников.
3) Центр описанной около треугольника окружности лежит в точке пересечения биссектрис углов треугольника.
НЕт, центр - это точка пересечения серединных перпендикуляров к сторонам треугольника
4) Площадь трапеции равна сумме оснований, умноженной на высоту.
НЕТ, площадь трапеции - это ПОЛУСУММА оснований умноженная на высоту.